Репетитор-онлайн — подготовка к ЦТ

10.4. Закон сохранения энергии при гармонических колебаниях

10.4.1. Сохранение энергии при механических гармонических колебаниях

Сохранение энергии при колебаниях математического маятника

При гармонических колебаниях полная механическая энергия системы сохраняется (остается постоянной).

Полная механическая энергия математического маятника складывается из кинетической энергии и потенциальной энергии:

Рис. 10.15

E = W _k + W _p,

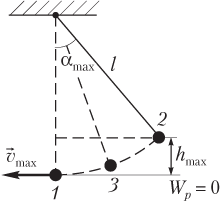
где W _k — кинетическая энергия, W _k = = mv ²/2; W _p — потенциальная энергия, W _p = mgh; m — масса груза; g — модуль ускорения свободного падения; v — модуль скорости груза; h — высота подъема груза над положением равновесия (рис. 10.15).

В Международной системе единиц энергия механической колебательной системы измеряется в джоулях (1 Дж).

При гармонических колебаниях математический маятник проходит ряд последовательных состояний, поэтому целесообразно рассмотреть энергию математического маятника в трех положениях (см. рис. 10.15):

Рис. 10.15

1) в положении равновесия (1) скорость тела имеет максимальное значение v _max, поэтому кинетическая энергия также максимальна:

$W_{k}^{max} = \frac{m v_{max}^{2}}{2}$ ;

потенциальная энергия равна нулю; полная энергия совпадает с максимальной кинетической энергией:

$E = W_{k}^{max}$ ;

2) в крайнем положении (2) тело поднято над исходным уровнем на максимальную высоту h _max, поэтому потенциальная энергия также максимальна:

$W_{p}^{max} = m g h_{max}$ ;

кинетическая энергия равна нулю; полная энергия совпадает с максимальной потенциальной энергией:

$E = W_{p}^{max}$ ;

3) в промежуточном положении (3) тело обладает мгновенной скоростью v и поднято над исходным уровнем на некоторую высоту h, поэтому полная энергия представляет собой сумму

$E = \frac{m v^{2}}{2} + m g h$ ,

где mv ²/2 — кинетическая энергия; mgh — потенциальная энергия; m — масса груза; g — модуль ускорения свободного падения; v — модуль скорости груза; h — высота подъема груза над положением равновесия.

При гармонических колебаниях математического маятника полная механическая энергия сохраняется:

E = const.

Значения полной энергии математического маятника в трех его положениях отражены в табл. 10.1.

№	Положение	W_p	W_k	E = W_p + W_k
1	Равновесие	0	$m v_{max}^{2} / 2$	$m v_{max}^{2} / 2$
2	Крайнее	mgh_max	0	mgh_max
3	Промежуточное (мгновенное)	mgh	mv²/2	mv²/2 + mgh

Значения полной механической энергии, представленные в последнем столбце табл. 10.1, имеют равные значения для любых положений маятника, что является математическим выражением закона сохранения полной механической энергии:

$\frac{m v_{max}^{2}}{2} = m g h_{max}$ ;

$\frac{m v_{max}^{2}}{2} = \frac{m v^{2}}{2} + m g h$ ;

$m g h_{max} = \frac{m v^{2}}{2} + m g h$ ,

где m — масса груза; g — модуль ускорения свободного падения; v — модуль мгновенной скорости груза в положении 3; h — высота подъема груза над положением равновесия в положении 3; v _max — модуль максимальной скорости груза в положении 1; h _max — максимальная высота подъема груза над положением равновесия в положении 2.

Угол отклонения нити математического маятника от вертикали (рис. 10.15) определяется выражением

$\cos α = \frac{l - h}{l} = 1 - \frac{h}{l}$ ,

где l — длина нити; h — высота подъема груза над положением равновесия.

Максимальный угол отклонения α_max определяется максимальной высотой подъема груза над положением равновесия h _max:

$\cos α_{\max} = 1 - \frac{h_{\max}}{l}$ .

Пример 11. Период малых колебаний математического маятника равен $\sqrt{0,9}$ с. На какой максимальный угол от вертикали будет отклоняться нить, если, проходя положение равновесия, шарик движется со скоростью, равной 1,5 м/с? Трение в системе отсутствует.

Решение. На рисунке показаны два положения математического маятника:

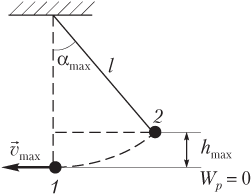
положение равновесия 1 (характеризуется максимальной скоростью шарика v _max);
крайнее положение 2 (характеризуется максимальной высотой подъема шарика h _max над положением равновесия).

Искомый угол определяется равенством

$\cos α_{max} = \frac{l - h_{max}}{l} = 1 - \frac{h_{max}}{l}$ ,

где l — длина нити маятника.

Максимальную высоту подъема шарика маятника над положением равновесия найдем из закона сохранения полной механической энергии.

Полная энергия маятника в положении равновесия и в крайнем положении определяется следующими формулами:

в положении равновесия —

$E_{1} = \frac{m v_{max}^{2}}{2}$ ,

где m — масса шарика маятника; v _max — модуль скорости шарика в положении равновесия (максимальная скорость), v _max = 1,5 м/с;

в крайнем положении —

E ₂ = mgh _max,

где g — модуль ускорения свободного падения; h _max — максимальная высота подъема шарика над положением равновесия.

Закон сохранения полной механической энергии:

$\frac{m v_{max}^{2}}{2} = m g h_{max}$ .

Выразим отсюда максимальную высоту подъема шарика над положением равновесия:

$h_{max} = \frac{v_{max}^{2}}{2 g}$ .

Длину нити определим из формулы для периода колебаний математического маятника

$T = 2 π \sqrt{\frac{l}{g}}$ ,

т.е. длина нити

$l = \frac{T^{2} g}{4 π^{2}}$ .

Подставим h _max и l в выражение для косинуса искомого угла:

$\cos α_{max} = 1 - \frac{2 π^{2} v_{max}^{2}}{g^{2} T^{2}}$

и произведем вычисление с учетом приблизительного равенства π² = 10:

$\cos α_{max} = 1 - \frac{2 \cdot 10 \cdot {(1,5)}^{2}}{10^{2} \cdot {(\sqrt{0,9})}^{2}} = 0,5$ .

Отсюда следует, что максимальный угол отклонения составляет 60°.

Строго говоря, при угле 60° колебания шарика не являются малыми и пользоваться стандартной формулой для периода колебаний математического маятника неправомерно.

Сохранение энергии при колебаниях пружинного маятника

Полная механическая энергия пружинного маятника складывается из кинетической энергии и потенциальной энергии:

Рис. 10.16

E = W _k + W _p,

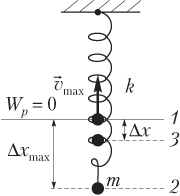
где W _k — кинетическая энергия, W _k = mv ²/2; W _p — потенциальная энергия, W _p = k(Δx)²/2; m — масса груза; v — модуль скорости груза; k — коэффициент жесткости (упругости) пружины; Δx — деформация (растяжение или сжатие) пружины (рис. 10.16).

В Международной системе единиц энергия механической колебательной системы измеряется в джоулях (1 Дж).

При гармонических колебаниях пружинный маятник проходит ряд последовательных состояний, поэтому целесообразно рассмотреть энергию пружинного маятника в трех положениях (см. рис. 10.16):

1) в положении равновесия (1) скорость тела имеет максимальное значение v _max, поэтому кинетическая энергия также максимальна:

$W_{k}^{max} = \frac{m v_{max}^{2}}{2}$ ;

потенциальная энергия пружины равна нулю, так как пружина не деформирована; полная энергия совпадает с максимальной кинетической энергией:

$E = W_{k}^{max}$ ;

2) в крайнем положении (2) пружина имеет максимальную деформацию (Δx _max), поэтому потенциальная энергия также имеет максимальное значение:

$W_{p}^{max} = \frac{k {(Δ x_{max})}^{2}}{2}$ ;

кинетическая энергия тела равна нулю; полная энергия совпадает с максимальной потенциальной энергией:

$E = W_{p}^{max}$ ;

3) в промежуточном положении (3) тело обладает мгновенной скоростью v, пружина имеет в этот момент некоторую деформацию (Δx), поэтому полная энергия представляет собой сумму

$E = \frac{m v^{2}}{2} + \frac{k {(Δ x)}^{2}}{2}$ ,

где mv ²/2 — кинетическая энергия; k(Δx)²/2 — потенциальная энергия; m — масса груза; v — модуль скорости груза; k — коэффициент жесткости (упругости) пружины; Δx — деформация (растяжение или сжатие) пружины.

При смещении груза пружинного маятника от положения равновесия на него действует возвращающая сила, проекция которой на направление движения маятника определяется формулой

F _x = −kx,

где x — смещение груза пружинного маятника от положения равновесия, x = ∆x, ∆x — деформация пружины; k — коэффициент жесткости (упругости) пружины маятника.

При гармонических колебаниях пружинного маятника полная механическая энергия сохраняется:

E = const.

Значения полной энергии пружинного маятника в трех его положениях отражены в табл. 10.2.

№	Положение	W_p	W_k	E = W_p + W_k
1	Равновесие	0	$m v_{max}^{2} / 2$	$m v_{max}^{2} / 2$
2	Крайнее	k(Δx_max)²/2	0	k(Δx_max)²/2
3	Промежуточное (мгновенное)	k(Δx)²/2	mv²/2	mv²/2 + k(Δx)²/2

Значения полной механической энергии, представленные в последнем столбце таблицы, имеют равные значения для любых положений маятника, что является математическим выражением закона сохранения полной механической энергии:

$\frac{m v_{max}^{2}}{2} = \frac{k {(Δ x_{max})}^{2}}{2}$ ;

$\frac{m v_{max}^{2}}{2} = \frac{m v^{2}}{2} + \frac{k {(Δ x)}^{2}}{2}$ ;

$\frac{k {(Δ x_{max})}^{2}}{2} = \frac{m v^{2}}{2} + \frac{k {(Δ x)}^{2}}{2}$ ,

где m — масса груза; v — модуль мгновенной скорости груза в положении 3; Δx — деформация (растяжение или сжатие) пружины в положении 3; v _max — модуль максимальной скорости груза в положении 1; Δx _max — максимальная деформация (растяжение или сжатие) пружины в положении 2.

Пример 12. Пружинный маятник совершает гармонические колебания. Во сколько раз его кинетическая энергия больше потенциальной в тот момент, когда смещение тела из положения равновесия составляет четверть амплитуды?

Решение. Сравним два положения пружинного маятника:

крайнее положение 1 (характеризуется максимальным смещением груза маятника от положения равновесия x _max);
промежуточное положение 2 (характеризуется промежуточными значениями смещения от положения равновесия x и скорости $\vec{v}$ ).

Полная энергия маятника в крайнем и промежуточном положениях определяется следующими формулами:

в крайнем положении —

$E_{1} = \frac{k {(Δ x_{max})}^{2}}{2}$ ,

где k — коэффициент жесткости (упругости) пружины; ∆x _max — амплитуда колебаний (максимальное смещение от положения равновесия), ∆x _max = A;

в промежуточном положении —

$E_{2} = \frac{k {(Δ x)}^{2}}{2} + \frac{m v^{2}}{2}$ ,

где m — масса груза маятника; ∆x — смещение груза от положения равновесия, ∆x = A/4.

Закон сохранения полной механической энергии для пружинного маятника имеет следующий вид:

$\frac{k {(Δ x_{max})}^{2}}{2} = \frac{k {(Δ x)}^{2}}{2} + \frac{m v^{2}}{2}$ .

Разделим обе части записанного равенства на k(∆x)²/2:

${(\frac{Δ x_{max}}{Δ x})}^{2} = 1 + \frac{m v^{2}}{2} \cdot \frac{2}{k Δ x^{2}} = 1 + \frac{W_{k}}{W_{p}}$ ,

где W _k — кинетическая энергия маятника в промежуточном положении, W _k = mv ²/2; W _p — потенциальная энергия маятника в промежуточном положении, W _p = k(∆x)²/2.

Выразим из уравнения искомое отношение энергий:

$\frac{W_{k}}{W_{p}} = {(\frac{Δ x_{max}}{Δ x})}^{2} - 1$

и рассчитаем его значение:

$\frac{W_{k}}{W_{p}} = {(\frac{A}{A / 4})}^{2} - 1 = 16 - 1 = 15$ .

В указанный момент времени отношение кинетической и потенциальной энергий маятника равно 15.

Физика