Предметы

Физика

Элементы статики и гидростатики

4.2. Элементы гидростатики

4.2.6. Гидравлический пресс

Теория Тренинг

Физика

Общий тест

4.2. Элементы гидростатики

4.2.6. Гидравлический пресс

Действие многих гидравлических устройств, в частности гидравлических прессов, основано на законе Паскаля (1653 г.).

Закон Паскаля: давление, оказываемое внешними силами на жидкость, передается жидкостью одинаково по всем направлениям.

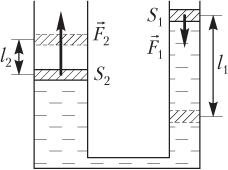
В гидравлическом прессе (рис. 4.17) в результате действия внешней силы на малый поршень жидкостью создается сила, действующая на большой поршень, по величине превышающая приложенную силу. Согласно закону Паскаля, давления под малым и большим поршнями одинаковы:

$p = \frac{F_{1}}{S_{1}} = \frac{F_{2}}{S_{2}}$ ,

Рис. 4.17

где F₁ — модуль внешней силы, действующей на малый поршень; F₂ — модуль силы, действующей со стороны жидкости на большой поршень; S₁ — площадь малого поршня; S₂ — площадь большого поршня. Поршни считаются невесомыми.

В гидравлическом прессе (см. рис. 4.17) сравнительно небольшой внешней силой, действующей на малый поршень, можно создать достаточно большое усилие (на большой поршень):

$F_{2} = F_{1} \frac{S_{2}}{S_{1}}$ ,

Формула справедлива, если в гидравлическом прессе отсутствуют потери энергии.

Рис. 4.17

При опускании малого поршня под действием силы ${\vec{F}}_{1}$ на расстояние l₁ большой поршень поднимается на расстояние l₂. При этом совершается полезная работа

A = F₂l₂.

Если на большом поршне стоит тело массой M, то указанная работа вычисляется по формуле

A = Mgl₂,

где g — модуль ускорения свободного падения.

В гидравлическом прессе реализуется принцип несжимаемости жидкости, математически выражаемый равенством

S₁l₁ = S₂l₂,

где S₁l₁ = V₁ — объем жидкости, вытесненный из узкого (малого) колена; S₂l₂ = V₂ — объем жидкости, перешедшей в широкое (большое) колено; S₁ и S₂ — площади малого и большого поршней соответственно; l₁ и l₂ — расстояния, на которые перемещаются малый и большой поршни соответственно.

Коэффициент полезного действия (КПД) гидравлического пресса определяется формулой

$η = \frac{A_{пол}}{A_{сов}} \cdot 100 % = \frac{F_{2} l_{2}}{F_{1} l_{1}} \cdot 100 %$ ,

где A_сов = F₁l₁ — совершенная (затраченная) работа; A_пол = F₂l₂ — полезная работа; F₁ и F₂ — модули сил, действующих на малый и на большой поршни соответственно; l₁ и l₂ — расстояния, на которые перемещаются малый и большой поршни соответственно.

Пример 30. Под действием некоторой силы малый поршень гидравлического пресса перемещается на расстояние 60 см, а большой поршень вместе с помещенным на него телом массой 40 кг — на расстояние 6,0 см. Коэффициент полезного действия гидравлического пресса составляет 80 %. Найти величину силы, действующей на малый поршень гидравлического пресса.

Решение. Коэффициент полезного действия гидравлического пресса определяется отношениями работ, совершаемых силами, действующими на поршни:

сила, действующая на малый поршень, совершает работу

A₁ = F₁l₁,

где F₁ — модуль силы, действующей на малый поршень гидравлического пресса; l₁ — расстояние, на которое перемещается малый поршень;

сила, действующая на большой поршень, совершает (полезную) работу по перемещению груза

A₂ = Mgl₂,

где M — масса груза, помещенного на большой поршень гидравлического пресса; g — модуль ускорения свободного падения; l₂ — расстояние, на которое перемещается большой поршень.

Подставляя в формулу для коэффициента полезного действия

$η = \frac{A_{2}}{A_{1}} \cdot 100 %$

выражения для указанных работ, получим:

$η = \frac{M g l_{2}}{F_{1} l_{1}} \cdot 100 %$ .

Выразим отсюда искомую величину — модуль силы, действующей на малый поршень пресса:

$F_{1} = \frac{M g l_{2}}{η l_{1}} \cdot 100 %$

и произведем вычисление:

$F_{1} = \frac{40 \cdot 10 \cdot 6,0 \cdot 10^{- 2}}{80 % \cdot 60 \cdot 10^{- 2}} \cdot 100 % = 50$ Н.

Пример 31. Площадь большого поршня гидравлического пресса, имеющего коэффициент полезного действия 75 %, в 15 раз превышает площадь малого поршня. Известно, что на малый поршень пресса действует сила 48 Н. Найти максимальную массу груза, которую может переместить большой поршень под действием указанной силы.

сила, действующая на малый поршень, совершает работу

A₁ = F₁l₁,

сила, действующая на большой поршень, совершает (полезную) работу по перемещению груза

A₂ = Mgl₂,

Подставляя в формулу для коэффициента полезного действия

$η = \frac{A_{2}}{A_{1}} \cdot 100 %$

выражения для указанных работ, получим:

$η = \frac{M g l_{2}}{F_{1} l_{1}} \cdot 100 %$ .

Выразим отсюда искомую величину — максимальную массу груза, которую может переместить большой поршень под действием указанной силы:

$M = \frac{η F_{1} l_{1}}{100 % \cdot g l_{2}}$ .

Максимальная масса груза зависит от отношения перемещений малого и большого поршней пресса (l₁/l₂). Данное отношение найдем из условия несжимаемости жидкости, т.е. из равенства объемов жидкости, перемещенной из узкого колена (V₁ = S₁l₁) в широкое (V₂ = S₂l₂):

S₁l₁ = S₂l₂,

где S₁ — площадь малого поршня; S₂ — площадь большого поршня.

С учетом

S₂ = 15S₁

отношение перемещений составляет:

$\frac{l_{1}}{l_{2}} = \frac{S_{2}}{S_{1}} = \frac{15 S_{1}}{S_{1}} = 15$ ,

а искомая масса равна

$M = \frac{15 η F_{1}}{100 % \cdot g} = \frac{15 \cdot 75 % \cdot 48}{100 % \cdot 10} = 54$ кг.

Таким образом, максимальная масса груза, которую может переместить большой поршень данного гидравлического пресса под действием силы, указанной в условии задачи, составляет 54 кг.