Физика
Сообщающимися называются сосуды, соединенные между собой каналом, заполненным жидкостью.
Для сообщающихся сосудов справедлив закон сообщающихся сосудов: высоты взаимно уравновешенных столбов разнородных жидкостей обратно пропорциональны плотностям этих жидкостей:
,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
Указанный закон справедлив в отсутствие сил поверхностного натяжения.
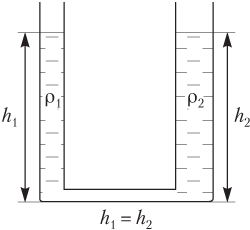
Если сообщающиеся сосуды заполнены однородной жидкостью
ρ1 = ρ2,
то свободные поверхности жидкости устанавливаются на одном уровне, независимо от формы сосудов (рис. 4.14):
h1 = h2,
где h1 — высота столба жидкости в левом колене; h2 — высота столба жидкости в правом колене сообщающихся сосудов.
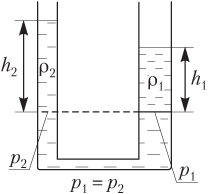
Если сообщающиеся сосуды заполнены разнородными жидкостями
ρ1 ≠ ρ2,
то свободные поверхности жидкостей, независимо от формы сосуда (рис. 4.15), устанавливаются так, что выполняется отношение
,
где h1 — высота столба жидкости плотностью ρ1; h2 — высота столба жидкости плотностью ρ2.
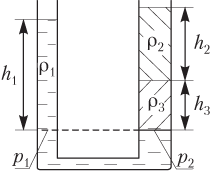
Если сообщающиеся сосуды заполнены несколькими жидкостями (например, как показано на рис. 4.16), то гидростатическое давление на одном уровне (отмеченном пунктиром) в левом колене определяется формулой
p1 = ρ1gh1,
в правом колене —
p2 = ρ2gh2 + ρ3gh3.
Равенство давлений на указанном уровне
p1 = p2
позволяет записать тождество:
ρ1h1 = ρ2h2 + ρ3h3.
Пример 28. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра второго, в нижней части соединены тонким шлангом. Площадь сечения узкого сосуда равна 10 см2. Система заполнена некоторым количеством жидкости плотностью 1,6 г/см3. Найти, на сколько миллиметров повысится уровень жидкости в каждом из сосудов, если в систему добавить 0,12 кг той же жидкости.
Решение. В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.
Добавление в систему некоторого количества жидкости массой m приводит к ее распределению по двум сосудам в соответствии с площадью их поперечного сечения:
- в первом сосуде оказывается масса жидкости
m1 = ρV1 = ρ∆h1S1,
где ρ — плотность жидкости; V1 = S1∆h1 — объем жидкости в первом сосуде; S1 — площадь поперечного сечения первого сосуда; ∆h1 — повышение уровня жидкости в первом сосуде;
- во втором сосуде оказывается масса жидкости
m2 = ρV2 = ρ∆h2S2,
где V2 = S2∆h2 — объем жидкости во втором сосуде; S2 — площадь поперечного сечения второго сосуда; ∆h2 — повышение уровня жидкости во втором сосуде.
Повышение уровней жидкости в обоих сосудах одинаково:
∆h1 = ∆h2 = ∆h,
поэтому масса жидкости, добавленной в систему, определяется формулой
m = m1 + m2 = ρ∆h(S1 + S2).
Выразим отсюда искомое значение ∆h:
.
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для первого (широкого) сосуда
,
- для второго (узкого) сосуда
,
где d1 = 2d2 — диаметр первого (широкого) сосуда; d2 — диаметр второго (узкого) сосуда.
Отношение площадей
позволяет найти площадь широкого сосуда:
S1 = 4S2.
Подставив S1 в формулу для ∆h
,
рассчитаем значение высоты, на которую повысится уровень жидкости в сосудах:
мм.
Пример 29. Два высоких сосуда, диаметр одного из которых в два раза больше диаметра другого, в нижней части соединены тонким шлангом. Площадь сечения широкого сосуда составляет 10 см2. Система заполнена жидкостью плотностью 6,0 г/см3. В узкий сосуд добавляют 0,12 кг жидкости плотностью 2,0 г/см3, а затем — 0,12 кг жидкости плотностью 4,0 г/см3. Найти разность уровней жидкостей в сосудах.
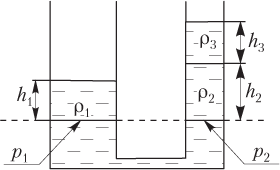
Решение. В сообщающихся сосудах неоднородная жидкость устанавливается на разных уровнях таким образом, что гидростатическое давление на выбранном уровне оказывается одинаковым:
p1 = p2,
где p1 — давление в широком сосуде; p2 — давление в узком сосуде.
На рисунке пунктирной линией обозначен уровень, на котором будем рассчитывать гидростатическое давление в широком и узком сосудах.
Гидростатическое давление на выбранном уровне:
- в широком сосуде
p1 = ρ1gh1,
где ρ1 — плотность жидкости, заполняющей систему изначально; g — модуль ускорения свободного падения; h1 — высота столба жидкости в широком сосуде;
- в узком сосуде
p2 = ρ2gh2 + ρ3gh3,
где ρ2 — плотность первой жидкости, добавленной в узкий сосуд; h2 — высота столба первой жидкости; ρ3 — плотность второй жидкости, добавленной в узкий сосуд; h3 — высота столба второй жидкости.
Равенство давлений на указанном уровне
ρ1gh1 = ρ2gh2 + ρ3gh3
позволяет определить высоту столба жидкости в широком сосуде:
,
где высоты жидкостей h2 и h3 определяются соответствующими массами и плотностями:
- для первой жидкости
;
- для второй жидкости
,
где S2 — площадь поперечного сечения узкого сосуда; m2 — масса первой жидкости, добавленной в узкий сосуд; m3 — масса второй жидкости, добавленной в узкий сосуд.
Подстановка h2 и h3 в формулу для h1 дает
.
Площади поперечного сечения сосудов связаны с их диаметрами формулой:
- для широкого сосуда
,
- для узкого сосуда
,
где d1 = 2d2 — диаметр широкого сосуда; d2 — диаметр узкого сосуда.
Отношение площадей
позволяет найти площадь узкого сосуда:
.
Таким образом, высота столба жидкости в широком сосуде определяется выражением
.
Высота столба жидкости над указанным уровнем в узком сосуде есть сумма:
.
Искомая разность верхних уровней жидкостей в узком (h2 + h3) и широком h1 сосудах рассчитывается по формуле
.
Произведем вычисление:
см.