Физика

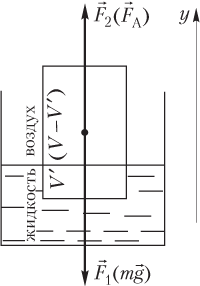
Пример 32. Некоторое тело обладает плотностью 1,2 г/см³. Если поместить его в жидкость, имеющую плотность 3,0 г/см³, то оно будет плавать на ее поверхности. Определить, какая часть плавающего тела при этом находится в воздухе.

Решение. На тело, плавающее в жидкости, действуют две силы, показанные на рисунке:

• сила тяжести, модуль которой определяется формулой

F₁ = mg = ρVg,

где m = ρV — масса тела; ρ — плотность тела; V — объем тела; g — модуль ускорения свободного падения;

• сила Архимеда, модуль которой определяется формулой

$F_2=F_{\text{A}}={\rho }_0{V}^{\prime }g$,

где ρ₀ — плотность жидкости; V′ — объем погруженной в жидкость части тела.

Под действием указанных сил тело находится в равновесии (плавает); условие равновесия определяется равенством

${\overrightarrow{F}}_1+{\overrightarrow{F}}_2=0$,

или в проекции на вертикальную ось

−F₁ + F₂ = 0.

Явный вид данного равенства

$\rho Vg={\rho }_0{V}^{\prime }g$

позволяет найти отношение объемов:

$\frac{V^{\prime }}{V}=\frac{\rho }{{\rho }_0}$.

Искомой величиной является доля объема тела, которая остается в воздухе, определяемая отношением:

$\eta =\frac{V-V^{\prime }}{V}=1-\frac{V^{\prime }}{V}$,

где (V − V′) — объем тела, находящийся в воздухе.

С учетом полученного отношения (V/V′) искомая доля составляет

$\eta =1-\frac{V^{\prime }}{V}=1-\frac{\rho }{{\rho }_0}=1-\frac{\mathrm{1,2}\cdot {10}^3}{\mathrm{3,0}\cdot {10}^3}=\mathrm{0,6}$.

Таким образом, доля объема тела, находящегося в воздухе, равна 0,6 (или 60 %).

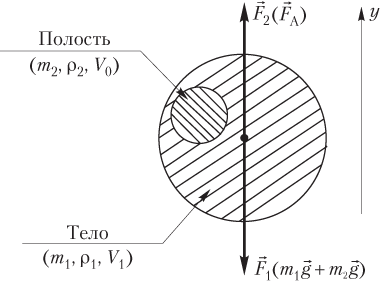
Пример 33. Тело, имеющее массу 4,0 кг, изготовлено из материала, плотность которого равна 6,4 г/см³. Из внутренней части тела удаляют определенную массу материала, а образовавшуюся полость заполняют другим материалом плотностью 1,4 г/см³. Найти объем полости, заполнение которой материалом указанной плотности обеспечит состояние безразличного равновесия тела в жидкости плотностью 2,0 г/см³.

Решение. Состояние безразличного равновесия тела в жидкости означает, что тело может плавать на любой глубине; тело при этом полностью погружено в жидкость.

В состоянии безразличного равновесия на тело действуют две силы, показанные на рисунке:

• сила тяжести, модуль которой определяется формулой

F₁ = mg = (m₁ + m₂)g,

где m = (m₁ + m₂) — масса «составного» тела; m₁ = (M − ∆m) — масса тела после удаления материала из полости; M — первоначальная масса тела (указанная в условии задачи); ∆m — масса материала, удаленного из полости; m₂ — масса материала, заполняющего полость; g — модуль ускорения свободного падения;

• сила Архимеда, модуль которой определяется формулой

F₂ = F_A = ρ₀Vg,

где ρ₀ — плотность жидкости; V — объем тела.

Под действием указанных сил тело находится в состоянии безразличного равновесия (плавает на любой глубине); условие равновесия определяется равенством

${\overrightarrow{F}}_1+{\overrightarrow{F}}_2=0$,

или в проекции на вертикальную ось

−F₁ + F₂ = 0.

В явном виде оно выглядит следующим образом:

(m₁ + m₂)g = ρ₀Vg.

Преобразуем данное выражение, заменив массы произведением плотностей и объемов:

• для массы m₁ —

m₁ = M − ∆m = M − ρ₁V₀;

• для массы m₂ —

m₂ = ρ₂V₀,

где ρ₁ — плотность материала, из которого состоит тело; ρ₂ — плотность материала, заполняющего полость; V₀ — объем полости.

Подстановка выражений, полученных для масс, в условие равновесия тела в жидкости дает равенство

M − ρ₁V₀ + ρ₂V₀ = ρ₀V,

позволяющее выразить искомую величину:

$V_0=\frac{M-{\rho }_{0}V}{{\rho }_1-{\rho }_2}$.

Объем тела найдем как отношение

$V=\frac{M}{{\rho }_1}$

и подставим в полученное выражение:

$V_0=\frac{M\left(1-\frac{{\rho }_0}{{\rho }_1}\right)}{{\rho }_1-{\rho }_2}=\frac{M}{{\rho }_1}\frac{{\rho }_1-{\rho }_0}{{\rho }_1-{\rho }_2}$.

Произведем вычисление:

$V_0=\frac{\mathrm{4,0}}{\mathrm{6,4}\cdot {10}^3}\cdot \frac{\mathrm{6,4}\cdot {10}^3-\mathrm{2,0}\cdot {10}^3}{\mathrm{6,4}\cdot {10}^3-\mathrm{1,4}\cdot {10}^3}=\mathrm{0,550}\cdot {10}^{-3}{\text{ м}}^3=550$ см³.

Таким образом, объем полости, обеспечивающий телу состояние безразличного равновесия в указанной жидкости, составляет 550 см³.

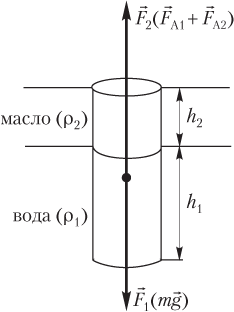
Пример 34. Прямой деревянный цилиндр плавает на поверхности воды так, что в воде находится 0,9 его высоты. На поверхность воды наливают слой масла плотностью 0,8 г/см³ таким образом, чтобы цилиндр оказался полностью погруженным в жидкость. Какая часть высоты цилиндра окажется погруженной в воду? Плотность воды составляет 1 г/см³_.

Решение. Рассмотрим условие равновесия цилиндра в жидкости:

• для цилиндра, плавающего в воде,

mg = F_A,

где m — масса цилиндра; g — модуль ускорения свободного падения; $F_{\text{A}}={\rho }_{1}g{V}^{\prime }$ — модуль силы Архимеда, действующей на цилиндр, плавающий в воде; ρ₁ — плотность воды; V′ — объем части цилиндра, погруженной в воду;

• для цилиндра, плавающего в двухслойной жидкости «вода — масло», как показано на рисунке,

mg = F_A1 + F_A2,

где F_A1 = ρ₁gV₁ — модуль силы Архимеда, действующей на цилиндр со стороны воды; V₁ — объем части цилиндра, погруженной в воду; F_A2 = ρ₂gV₂ — модуль силы Архимеда, действующей на цилиндр со стороны масла; V₂ — объем части цилиндра, погруженной в масло.

Объемы выразим как произведение соответствующих высот на площадь поперечного сечения цилиндра S:

• для цилиндра V

V = hS;

• для части цилиндра, погруженной в воду V₁,

V₁ = h₁S;

• для части цилиндра, погруженной в масло V₂,

V₂ = h₂S,

где h — высота цилиндра; h₁ — высота части цилиндра, погруженной в воду; h₂ — высота части цилиндра, погруженной в масло.

Искомой величиной является отношение

$\eta =\frac{h_1}{h}=\frac{V_1}{V}$.

Для определения данного отношения запишем систему уравнений из условий равновесия цилиндра в воде и в двухслойной жидкости «вода — масло», подставив выражения для сил и представив массу цилиндра в виде произведения

m = ρV,

где ρ — плотность материала цилиндра.

Указанная система имеет вид:

$\begin{array}{l}\rho Vg={\rho }_{1}g{V}^{\prime };\\ \rho Vg={\rho }_{1}g{V}_1+{\rho }_{2}g{V}_2,\end{array}\}$

или с учетом (V′/V = 0,9):

$\begin{array}{l}\rho =\mathrm{0,9}{\rho }_1;\\ \rho V={\rho }_1{V}_1+{\rho }_2{V}_2.\end{array}\}$

Дополним систему уравнением

V = V₁ + V₂.

Подстановка первого уравнения во второе дает:

$\begin{array}{l}\mathrm{0,9}{\rho }_{1}V={\rho }_1{V}_1+{\rho }_2{V}_2;\\ V=V_1+V_2.\end{array}\}$

Исключая величину V₂, получим равенство:

$\frac{{\rho }_1}{{\rho }_2}(\mathrm{0,9}V-V_1)=V-V_1$.

Деление обеих частей равенства на V

$\frac{{\rho }_1}{{\rho }_2}\left(\mathrm{0,9}-\frac{V_1}{V}\right)=1-\frac{V_1}{V}$

позволяет найти искомую величину:

$\eta =\frac{V_1}{V}=\frac{\mathrm{0,9}{\rho }_1-{\rho }_2}{{\rho }_1-{\rho }_2}=\frac{\mathrm{0,9}\cdot \mathrm{1,0}\cdot {10}^3-\mathrm{0,8}\cdot {10}^3}{\mathrm{1,0}\cdot {10}^3-\mathrm{0,8}\cdot {10}^3}=\mathrm{0,5}$.

Таким образом, цилиндр плавает, погрузившись в воду на половину своей высоты.