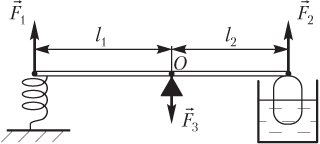Предметы

Физика

Элементы статики и гидростатики

4.1. Элементы статики

4.1.5. Условие равновесия абсолютно твердого тела

Теория Тренинг

Физика

Общий тест

4.1. Элементы статики

4.1.5. Условие равновесия абсолютно твердого тела

Если под действием нескольких сил тело может двигаться не только поступательно, но и вращаться относительно некоторой оси, то при решении задач указанное тело нельзя рассматривать как материальную точку. Для того чтобы абсолютно твердое тело находилось в равновесии, необходимо отсутствие не только линейного, но и углового ускорения центра масс.

Центр масс системы материальных точек (абсолютно твердого тела) не имеет углового ускорения в некоторой ИСО, если результирующий момент всех действующих на систему (тело) сил относительно некоторой точки равен нулю:

$\vec{M} = 0$ .

Результирующий момент нескольких сил — это векторная сумма моментов каждой из сил, действующих на тело:

$\vec{M} = {\vec{M}}_{1} + {\vec{M}}_{2} + ... + {\vec{M}}_{N}$ ,

где ${\vec{M}}_{1}$ — момент силы ${\vec{F}}_{1}$ относительно некоторой точки; ${\vec{M}}_{2}$ — момент силы ${\vec{F}}_{1}$ относительно той же точки и т.п.

Для сложения нескольких моментов сил, действующих на тело, используют следующий алгоритм:

1) вычисляют модули моментов каждой из сил по формулам

M₁ = r₁F₁ sin α₁,

M₂ = r₂F₂ sin α₂,

...,

M_N = r_NF_N sin α_N;

2) определяют направление каждого момента по правилу правого винта;

3) выбирают направление предполагаемой оси вращения Oz;

4) находят проекции каждого из моментов на выбранную ось:

моменты, совпадающие по направлению с осью вращения, имеют положительные проекции;
моменты, направленные противоположно ей, — отрицательные;

5) сумму проекций моментов относительно оси записывают в алгебраическом виде:

M_z = M₁_z + M₂_z + ... + M_Nz;

6) определяют величину результирующего момента как модуль найденной проекции:

$M = | M_{z} | .$

Если абсолютно твердое тело находится в равновесии (покоится относительно выбранной ИСО), то

точка, через которую проходит предполагаемая ось вращения, выбирается исходя из соображений удобства;
моменты всех сил, приложенных к телу, рассчитываются относительно одной и той же выбранной точки или оси;
моменты тех сил, точки приложения которых лежат на выбранной оси, обращаются в нуль.

Именно поэтому при решении задач следует выбирать предполагаемую ось вращения таким образом, чтобы она проходила (перпендикулярно плоскости чертежа) через точку приложения сил, исключенных из рассмотрения в данной задаче.

Когда предполагаемая ось вращения проходит через центр тяжести системы, результирующий момент всех сил тяжести относительно указанной оси равен нулю:

$\vec{M} = 0$ .

Если в центр тяжести поместить опору, то абсолютно твердое тело (система материальных точек) под действием сил тяжести будет находиться в равновесии.

Пример 13. На одном конце горизонтального однородного стержня длиной 4,0 м закреплена точечная масса 0,10 кг, а на другом — точечная масса 0,60 кг. Определить модуль результирующего момента сил тяжести относительно горизонтальной оси, проходящей перпендикулярно стержню через его центр.

Решение. Система состоит из стержня и двух точечных масс, закрепленных на его концах. Стержень является однородным; следовательно, центр тяжести стержня находится в его середине.

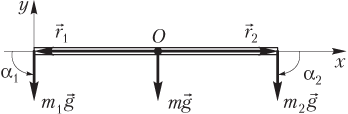
На рисунке показаны:

сила тяжести, действующая на стержень $m \vec{g}$ ;
сила тяжести, действующая на точечную массу, закрепленную на левом конце стержня $m_{1} \vec{g}$ ;
сила тяжести, действующая на точечную массу, закрепленную на правом конце стержня $m_{2} \vec{g}$ ;
радиус-векторы ${\vec{r}}_{1}$ и ${\vec{r}}_{2}$ , проведенные от оси вращения к точкам приложения сил $m_{1} \vec{g}$ и $m_{2} \vec{g}$ соответственно;
углы α₁ и α₂ между парами векторов ( ${\vec{r}}_{1}$ , $m_{1} \vec{g}$ ) и ( ${\vec{r}}_{2}$ , $m_{2} \vec{g}$ ) соответственно.

Модули моментов сил тяжести относительно указанной оси определяются следующим образом:

стержня —

M = 0,

так как сила $m \vec{g}$ приложена к оси вращения, т.е. радиус-вектор, проведенный от оси вращения к точке приложения указанной силы, равен нулю;

точечной массы, закрепленной на левом конце стержня,

M₁ = m₁gr₁ sin α₁,

где m₁ — масса, закрепленная на левом конце стержня; g — модуль ускорения свободного падения; r₁ = l/2 — модуль радиус-вектора, проведенного от оси вращения к точке приложения силы $m_{1} \vec{g}$ ; l — длина стержня; $α_{1} = 90 °$ — угол между вектором силы $m_{1} \vec{g}$ и радиус-вектором ${\vec{r}}_{1}$ ;

точечной массы, закрепленной на правом конце стержня,

$M_{2} = m_{2} g r_{2} \sin α_{2}$ ,

где m₂ — масса, закрепленная на правом конце стержня; r₂ = l/2 — модуль радиус-вектора, проведенного от оси вращения к точке приложения силы $m_{2} \vec{g}$ ; $α_{2} = 90 °$ — угол между вектором силы $m_{2} \vec{g}$ и радиус-вектором ${\vec{r}}_{2}$ .

Направления моментов сил тяжести определим по правилу правого винта:

для точечной массы, закрепленной на левом конце стержня, — «к нам» (вращение правого винта производим от ${\vec{r}}_{1}$ к $m_{1} \vec{g}$ по наименьшему углу, т.е. против часовой стрелки);
для точечной массы, закрепленной на правом конце стержня, — «от нас» (вращение правого винта производим от ${\vec{r}}_{2}$ к $m_{2} \vec{g}$ по наименьшему углу, т.е. по часовой стрелке).

Направим ось Oz за плоскость чертежа, т.е. «от нас». Тогда проекция момента ${\vec{M}}_{1}$ на указанную ось будет отрицательной, а проекция момента ${\vec{M}}_{2}$ — положительной:

M₁_z = −M₁; M₂_z = −M₂.

Проекция результирующего момента всех сил тяжести системы на указанную координатную ось определяется, таким образом, выражением

M_z = −M₁ + M₂,

или в явном виде

$M_{z} = - m_{1} g \frac{l}{2} \sin 90 ° + m_{2} g \frac{l}{2} \sin 90 ° = \frac{(m_{2} - m_{1}) g l \sin 90 °}{2}$ .

Модуль результирующего момента сил тяжести равен модулю его проекции на указанную ось:

$M = | M_{z} | = \frac{| m_{2} - m_{1} | g l \sin 90 °}{2} = \frac{| 0,60 - 0,10 | \cdot 10 \cdot 4,0 \cdot 1}{2} = 10$ Н ⋅ м

Пример 14. Палочка массой 0,70 кг в виде тонкого однородного цилиндра длиной 60 см и площадью поперечного сечения 3,0 см² закреплена на оси вращения верхним концом. Нижний конец палочки опущен в воду плотностью 1,0 г/см³ и погружен в нее на 1/3 длины. Вычислить модуль результирующего момента силы Архимеда и силы тяжести относительно горизонтальной оси, проходящей перпендикулярно палочке через ее верхний конец, при отклонении палочки от вертикали на 30°.

Решение. Палочка является однородной, поэтому сила тяжести приложена к ее середине. Сила Архимеда действует только на погруженную в воду часть палочки и приложена к середине погруженной части.

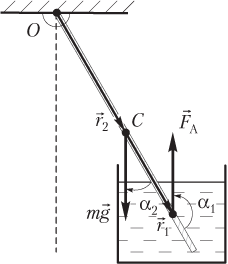
На рисунке показаны:

сила Архимеда ${\vec{F}}_{A}$ и сила тяжести $m \vec{g}$ ;
радиус-векторы, проведенные от оси вращения к точке приложения силы Архимеда ${\vec{r}}_{1}$ и силы тяжести ${\vec{r}}_{2}$ ;
углы α₁ и α₂ между парами векторов ( ${\vec{r}}_{1}$ , ${\vec{F}}_{A}$ ) и ( ${\vec{r}}_{2}$ , $m \vec{g}$ ) соответственно.

Модули моментов силы Архимеда и силы тяжести относительно указанной оси определяются следующим образом:

силы Архимеда

M₁ = F_Ar₁ sin α₁,

где $F_{A} = ρ_{0} g V^{'}$ — модуль силы Архимеда; ρ₀ — плотность воды; g — модуль ускорения свободного падения; $V^{'} = \frac{1}{3} V$ — объем погруженной части палочки; V — объем палочки; $r_{1} = \frac{5}{6} l$ — модуль радиус-вектора точки приложения силы Архимеда относительно заданной оси; l — длина палочки; α₁ = 180° − 30° = 150° — угол между вектором силы Архимеда и радиус-вектором;

силы тяжести

M₂ = mgr₂ sin α₂,

где m — масса палочки; $r_{2} = \frac{1}{2} l$ — модуль радиус-вектора точки приложения силы тяжести относительно заданной оси; α₂ = 30° — угол между вектором силы тяжести и радиус-вектором.

Направления моментов силы Архимеда и силы тяжести определим по правилу правого винта:

силы Архимеда — «к нам» (вращение правого винта производим от ${\vec{r}}_{1}$ к ${\vec{F}}_{A}$ по наименьшему углу, т.е. против часовой стрелки);
силы тяжести — «от нас» (вращение правого винта производим от ${\vec{r}}_{2}$ к $m \vec{g}$ по наименьшему углу, т.е. по часовой стрелке).

Направим ось Oz «к нам». Тогда проекция момента ${\vec{M}}_{1}$ на указанную ось будет положительной, а проекция момента ${\vec{M}}_{2}$ — отрицательной:

M₁_z = M₁; M₂_z = −M₂.

Проекция результирующего момента указанных сил на данную координатную ось определяется, таким образом, выражением

M_z = M₁ − M₂,

или в явном виде

$M_{z} = ρ_{0} g \frac{1}{3} V \frac{5}{6} l \sin 150 ° - m g \frac{l}{2} \sin 30 ° =$

$= g \frac{l}{2} (\frac{5}{9} ρ_{0} V \sin 150 ° - m \sin 30 °)$ .

C учетом

равенства $sin 150 ° = sin 30 °$ ;
выражения для объема V = Sl

проекция результирующего момента принимает вид:

$M_{z} = g \frac{l}{2} \sin 30 ° (\frac{5}{9} ρ_{0} S l - m)$ ,

где S — площадь поперечного сечения палочки.

Модуль результирующего момента указанных сил равен модулю его проекции на указанную ось:

$M = | M_{z} | = g \frac{l}{2} \sin 30 ° | \frac{5}{9} ρ_{0} S l - m |$ .

Произведем вычисление:

$M = \frac{10 \cdot 60 \cdot 10^{- 2} \cdot 0,5}{2} | \frac{5}{9} \cdot 1,0 \cdot 10^{3} \cdot 3,0 \cdot 10^{- 4} \cdot 60 \cdot 10^{- 2} - 0,70 | =$

$= 0,90$ Н ⋅ м.

Пример 15. Однородный стержень, подвешенный на нити к потолку за один конец, другим концом касается пола. Стержень и нить имеют одинаковую длину и образуют между собой угол 60°. Определить коэффициент трения между стержнем и полом.

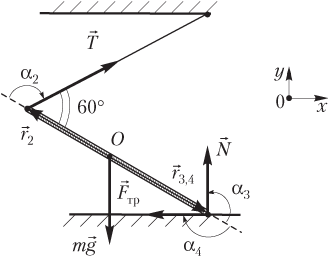
Решение. Под действием сил, показанных на рисунке, стержень находится в равновесии.

Стержень является однородным, поэтому центр тяжести стержня находится в его середине. Однако масса стержня не задана в условии задачи. Следовательно, целесообразно выбрать предполагаемую ось вращения таким образом, чтобы она проходила через середину стержня перпендикулярно плоскости чертежа (точка O).

Запишем условие равновесия стержня относительно указанной оси:

${\vec{M}}_{1} + {\vec{M}}_{2} + {\vec{M}}_{3} + {\vec{M}}_{4} = 0$ ,

где ${\vec{M}}_{1}$ — момент силы тяжести; ${\vec{M}}_{2}$ — момент силы натяжения нити; ${\vec{M}}_{3}$ — момент силы нормальной реакции опоры; ${\vec{M}}_{4}$ — момент силы трения.

Нить и стержень образуют правильный треугольник, поэтому модули указанных моментов определяются следующими формулами:

силы тяжести

M₁ = 0,

так как сила тяжести приложена к оси вращения (радиус-вектор, проведенный от оси вращения к точке приложения силы тяжести, равен нулю);

силы натяжения нити

M₂ = Tr₂ sin α₂,

где T — модуль силы натяжения нити; r₂ = l/2 — модуль радиус-вектора, проведенного от оси вращения (середина стержня) к точке приложения указанной силы (верхний конец стержня); l — длина стержня; α₂ = 180° − 60° = 120°;

силы нормальной реакции опоры

M₃ = Nr₃ sin α₃,

где N — модуль силы нормальной реакции опоры; r₃ = l/2 — модуль радиус-вектора, проведенного от оси вращения (середина стержня) к точке приложения указанной силы (нижний конец стержня); α₃ = 180° − 60° = 120°;

силы трения

M₄ = F_трr₄ sin α₄,

где F_тр = µN — модуль максимальной силы трения покоя; µ — коэффициент трения; r₄ = l/2 — модуль радиус-вектора, проведенного от оси вращения (середина стержня) к точке приложения указанной силы (нижний конец стержня); α₄ = 180° − 30° = 150°.

Направления моментов указанных сил определим по правилу правого винта:

силы натяжения нити — «от нас» (вращение правого винта производим от ${\vec{r}}_{2}$ к $\vec{T}$ по наименьшему углу, т.е. по часовой стрелке);
силы нормальной реакции опоры — «к нам» (вращение правого винта производим от ${\vec{r}}_{3}$ к $\vec{N}$ по наименьшему углу, т.е. против часовой стрелки);
силы трения — «от нас» (вращение правого винта производим от ${\vec{r}}_{4}$ к ${\vec{F}}_{тр}$ по наименьшему углу, т.е. по часовой стрелке).

Выберем направление оси вращения. Ось целесообразно направить в ту сторону, в которую направлено большинство моментов сил; в данном случае — «от нас». Тогда знак проекций моментов сил на указанную ось будет следующим:

проекции момента силы натяжения нити — положительным: M₂_z = M₂;
проекции момента силы нормальной реакции опоры — отрицательным: M₃_z = −M₃;
проекции момента силы трения — положительным: M₄_z = M₄.

Условие равновесия стержня с учетом сказанного приобретает вид:

M₂ − M₃ + M₄ = 0,

или

$T \frac{l}{2} \sin 120 ° - N \frac{l}{2} \sin 120 ° + μ N \frac{l}{2} \sin 150 ° = 0$ .

Упрощение дает формулу

T sin 60° − N sin 60° + µN sin 30° = 0.

Дополним систему условием отсутствия поступательного движения центра масс стержня:

$m \vec{g} + \vec{T} + \vec{N} + {\vec{F}}_{тр} = 0$ ,

или в проекциях на координатные оси:

$\begin{array}{l} O x : T \cos 30 ° - F_{тр} = 0; \\ O y : T \sin 30 ° + N - m g = 0. \end{array}}$

С учетом F_тр = µN полная система уравнений выглядит следующим образом:

$\begin{array}{l} T \sin 60 ° - N \sin 60 ° + μ N \sin 30 ° = 0; \\ T \cos 30 ° - μ N = 0; \\ T \sin 30 ° + N - m g = 0. \end{array}}$

Выразим отношение (T/N) из первого и второго уравнений системы:

$\begin{array}{l} \frac{T}{N} = \frac{\sin 60 ° - μ \sin 30 °}{\sin 60 °} = 1 - μ \frac{\sin 30 °}{\sin 60 °} = 1 - \frac{μ}{\sqrt{3}}; \\ \frac{T}{N} = \frac{μ}{\cos 30 °} = \frac{2 μ}{\sqrt{3}} . \end{array}}$

Равенство левых частей уравнений позволяет записать равенство их правых частей:

$1 - \frac{μ}{\sqrt{3}} = \frac{2 μ}{\sqrt{3}}$ .

Искомый коэффициент трения, таким образом, составляет:

$μ = \frac{\sqrt{3}}{3} \approx 0,58$ .

Пример 16. Легкая лестница длиной 12,0 м приставлена к гладкой стене под углом 45° к полу. Максимальная сила трения между лестницей и полом равна 532 Н. На какую высоту может подняться по лестнице человек массой 75,0 кг, прежде чем лестница начнет скользить?

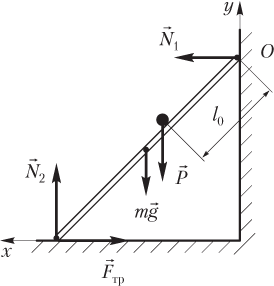
Решение. Под действием сил, показанных на рисунке, лестница находится в равновесии.

Предполагаемую ось вращения выбираем проходящей через верхний конец лестницы перпендикулярно плоскости чертежа (через точку O).

Запишем условия равновесия лестницы в виде системы уравнений:

$\begin{array}{l} {\vec{N}}_{1} + {\vec{N}}_{2} + {\vec{F}}_{тр} + \vec{P} = 0; \\ {\vec{M}}_{1} + {\vec{M}}_{2} + {\vec{M}}_{3} + {\vec{M}}_{4} = 0, \end{array}}$

где ${\vec{N}}_{1}$ — сила нормальной реакции стены, действующая на верхний конец лестницы; ${\vec{N}}_{2}$ — сила нормальной реакции пола, действующая на нижний конец лестницы; ${\vec{F}}_{тр}$ — сила трения между лестницей и полом; $\vec{P}$ — вес человека; ${\vec{M}}_{1}$ — момент силы нормальной реакции стены; ${\vec{M}}_{2}$ — момент силы нормальной реакции пола; ${\vec{M}}_{3}$ — момент силы трения между лестницей и полом; ${\vec{M}}_{4}$ — момент веса человека.

Силу тяжести лестницы $m \vec{g}$ считаем равной нулю, так как лестница является легкой; силу трения между лестницей и стеной также считаем равной нулю, так как стена является гладкой.

Модули моментов и их направления определяются следующими формулами:

силы нормальной реакции стены

M₁ = N₁ ⋅ 0 = 0,

так как сила нормальной реакции стены приложена к оси вращения;

силы нормальной реакции пола

$\otimes M_{2} = N_{2} l \sin 135 °$ ,

где l — длина лестницы;

силы трения

$⊙ M_{3} = F_{тр} l \sin 135 °$ ,

где F_тр — модуль максимальной силы трения покоя;

веса человека

$⊙ M_{4} = P l_{0} \sin 45 °$ ,

где P = Mg — вес человека; M — масса человека; g — модуль ускорения свободного падения; l₀ — расстояние от оси вращения до человека.

Пусть ось вращения Oz направлена «к нам», а координатные оси Ox и Oy — так, как показано на рисунке. Тогда условия равновесия в проекциях на координатные оси имеют вид:

$\begin{array}{l} O x : N_{1} - F_{тр} = 0; \\ O y : N_{2} - M g = 0; \\ O z : - N_{2} l + F_{тр} l + M g l_{0} = 0. \end{array}}$

Решение системы относительно величины l₀ дает:

$l_{0} = l (1 - \frac{F_{тр}}{M g})$ ,

что позволяет рассчитать искомую высоту подъема по формуле

$h = (l - l_{0}) \sin 45 ° = \frac{F_{тр}}{M g} l \sin 45 °$ .

Произведем вычисление:

$h = \frac{532}{75,0 \cdot 10} \cdot 12,0 \cdot \frac{\sqrt{2}}{2} \approx 6, 00$ м.

Пример 17. Легкое коромысло длиной 2,4 м закреплено на оси. Одно плечо коромысла длиной 1,4 м на 8,0 см сжимает пружину с коэффициентом жесткости 0,80 кН/м. Другое плечо коромысла топит в воде поплавок массой 1,0 кг. Определить объем подводной части поплавка, если коромысло находится в равновесии. Плотность воды составляет 1,0 г/см³.

Решение. На рисунке показаны плечи коромысла и силы, действующие на него:

сила упругости ${\vec{F}}_{1}$ , подъемная сила ${\vec{F}}_{2}$ и некоторая сила ${\vec{F}}_{3}$ , возникающая в опоре;
длинное плечо коромысла l₁ (от оси вращения до точки приложения силы упругости), короткое плечо коромысла l₂ (от оси вращения до точки приложения подъемной силы).

Под действием указанных сил коромысло находится в равновесии.

Модули моментов силы упругости и подъемной силы относительно оси, проходящей через точку O перпендикулярно плоскости чертежа, определяются следующим образом:

силы упругости

M₁ = F₁l₁ sin α₁,

где F₁ = k∆l — модуль силы упругости; k — коэффициент упругости пружины; ∆l — деформация (сжатие) пружины; l₁ — длина длинного плеча коромысла; α₁ = 90° — угол между вектором силы упругости и радиус-вектором, проведенным от оси вращения к точке приложения силы упругости;

подъемной силы

M₂ = F₂l₂ sin α₂,

где F₂ = F_A − mg — модуль подъемной силы; F_A = ρ₀gV′ — модуль силы Архимеда; ρ₀ — плотность воды; V′ — объем погруженной части поплавка; m — масса поплавка; g — модуль ускорения свободного падения; l₂ = 1,0 м — длина короткого плеча коромысла; α₂ = 90° — угол между вектором подъемной силы и радиус-вектором, проведенным от оси вращения к точке приложения подъемной силы;

силы, возникающей в опоре,

M₃ = 0,

так как данная сила приложена к оси вращения.

Направления моментов силы упругости и подъемной силы определим по правилу правого винта:

силы упругости — «от нас» (вращение правого винта производим по часовой стрелке);
подъемной силы — «к нам» (вращение правого винта производим против часовой стрелки).

Направим ось Oz «от нас». Тогда проекция момента ${\vec{M}}_{1}$ на указанную ось будет положительной, а проекция момента ${\vec{M}}_{2}$ — отрицательной:

$M_{1 z} = M_{1} = k (Δ l) l_{1} \sin 90 ° = k (Δ l) l_{1}$ ;

$M_{2 z} = - M_{2} = - (F_{A} - m g) l_{2} \sin 90 ° = - (F_{A} - m g) l_{2}$ .

$M_{z} = M_{1} - M_{2} = k (Δ l) l_{1} - (F_{A} - m g) l_{2}$ .

Коромысло находится в равновесии, поэтому проекция результирующего момента на указанную ось вращения равна нулю:

M_z = 0,

или

k(∆l)l₁ − (F_A − mg)l₂ = 0.

Данное уравнение, записанное с учетом явного вида силы Архимеда,

$k (Δ l) l_{1} = (ρ_{0} V^{'} - m) g l_{2}$

позволяет получить формулу для определения объема погруженной части поплавка:

$V^{'} = \frac{k (Δ l)}{ρ_{0} g} \frac{l_{1}}{l_{2}} + \frac{m}{ρ_{0}}$

и рассчитать его величину:

$V^{'} = \frac{0,80 \cdot 10^{3} \cdot 8,0 \cdot 10^{- 2}}{1,0 \cdot 10^{3} \cdot 10} \cdot \frac{1,4}{1,0} + \frac{1,0}{1,0 \cdot 10^{3}} \approx 10 \cdot 10^{- 3} м^{3} = 10$ дм³.

Пример 18. Однородный стержень массой 180 кг и объемом 50,0 дм³ лежит на горизонтальном дне сосуда, наполненного некоторой жидкостью. Определить минимальное значение модуля силы, которая может приподнять конец стержня. Плотность жидкости в сосуде составляет 2,00 г/см³.

Решение. Стержень приподнимается вертикальной силой $\vec{F}$ , приложенной к правому концу стержня, как показано на рисунке.

Запишем условие равновесия стержня в следующем виде:

${\vec{M}}_{1} + {\vec{M}}_{2} + {\vec{M}}_{3} + {\vec{M}}_{4} + {\vec{M}}_{5} = 0$ ,

где ${\vec{M}}_{1}$ — момент силы нормальной реакции дна сосуда; ${\vec{M}}_{2}$ — момент силы трения; ${\vec{M}}_{3}$ — момент силы тяжести; ${\vec{M}}_{4}$ — момент силы Архимеда; ${\vec{M}}_{5}$ — момент искомой силы, приподнимающей конец стержня.

Все моменты рассчитываются относительно предполагаемой оси вращения, проходящей через нижний конец стержня (через точку O) перпендикулярно плоскости чертежа.

Модули указанных моментов и их направления определяются следующими формулами:

силы нормальной реакции дна сосуда

M₁ = N ⋅ 0 = 0,

так как сила нормальной реакции дна сосуда приложена к оси вращения;

силы трения

M₂ = F_тр ⋅ 0 = 0,

так как сила трения также приложена к оси вращения;

силы тяжести

$\otimes M_{3} = m g \frac{l}{2} \sin α_{1}$ ,

где m — масса стержня; g — модуль ускорения свободного падения; l — длина стержня; α₁ — угол между радиус-вектором, проведенным от оси вращения к точке приложения силы тяжести (середина стержня), и указанной силой;

силы Архимеда

$⊙ M_{4} = F_{A} \frac{l}{2} \sin α_{2}$ ,

где F_A = ρ₀gV — модуль силы Архимеда; ρ₀ — плотность жидкости; V — объем стержня; α₂ — угол между радиус-вектором, проведенным от оси вращения к точке приложения силы Архимеда (середина стержня), и указанной силой;

силы, способной приподнять конец стержня,

$⊙ M_{5} = F l \sin α_{2}$ ,

где F — модуль искомой силы; α₂ — угол между радиус-вектором, проведенным от оси вращения к точке приложения искомой силы (правый конец стержня), и указанной силой.

Пусть ось вращения Oz направлена «к нам». Тогда условие равновесия в проекции на указанную ось:

−M₃ + M₄ + M₅ = 0,

или в явном виде:

$- m g \frac{l}{2} \sin α_{1} + F_{A} \frac{l}{2} \sin α_{2} + F l \sin α_{2} = 0$ .

Упрощение уравнения с учетом равенства

sin α₂ = sin(180° − α₁) = sin α₁

дает:

$- \frac{m g}{2} + \frac{F_{A}}{2} + F = 0$ ,

или

$F = \frac{1}{2} (m g - F_{A}) = \frac{g}{2} (m - ρ_{0} V)$ .

Произведем вычисление:

$F = \frac{10}{2} (180 - 2,00 \cdot 10^{3} \cdot 50,0 \cdot 10^{- 3}) = 400$ Н.

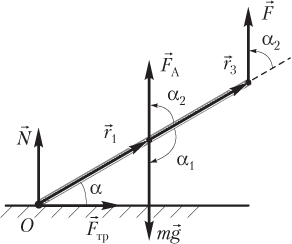
Пример 19. Диск массой 5,2 кг находится на наклонной плоскости с углом при основании 60°. Качение диска предотвращено трением и горизонтально расположенной нитью, которая одним концом прикреплена к вершине наклонной плоскости, а другим — к самой высокой точке диска. Найти модуль силы натяжения нити.

Решение. Под действием сил, показанных на рисунке, диск находится в равновесии.

Предполагаемая ось вращения проходит через точку диска, соприкасающуюся с наклонной плоскостью, перпендикулярно плоскости чертежа (через точку O).

Запишем условие равновесия диска в следующем виде:

${\vec{M}}_{1} + {\vec{M}}_{2} + {\vec{M}}_{3} + {\vec{M}}_{4} = 0$ ,

где ${\vec{M}}_{1}$ — момент силы нормальной реакции наклонной плоскости $\vec{N}$ ; ${\vec{M}}_{2}$ — момент силы трения ${\vec{F}}_{тр}$ ; ${\vec{M}}_{3}$ — момент силы тяжести $(m \vec{g})$ ; ${\vec{M}}_{4}$ — момент силы натяжения нити $\vec{T}$ .

Модули указанных моментов и их направления определяются следующими формулами:

силы нормальной реакции наклонной плоскости

M₁ = N ⋅ 0 = 0,

так как сила нормальной реакции наклонной плоскости приложена к оси вращения;

силы трения

M₂ = F_тр ⋅ 0 = 0,

так как сила трения также приложена к оси вращения;

силы тяжести

$⊙ M_{3} = m g R \sin θ$ ,

где m — масса диска; g — модуль ускорения свободного падения; R — радиус диска;

силы натяжения нити

$\otimes M_{4} = T x \sin β$ ,

где T — модуль силы натяжения нити; x — расстояние от оси вращения до точки приложения указанной силы.

Пусть ось вращения Oz направлена «к нам». Тогда условие равновесия в проекции на указанную ось запишем в виде:

mgR sin θ − Tx sin β = 0.

Отсюда следует, что модуль искомой силы натяжения нити определяется выражением

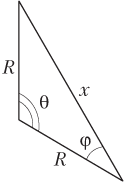
$T = m g \frac{R}{x} \frac{\sin θ}{\sin β} = m g \frac{R}{(x / \sin θ)} \frac{1}{\sin β}$ .

Для вычисления модуля силы натяжения нити по данной формуле необходимо установить значение выражения

$\frac{R}{(x / \sin θ)} \frac{1}{\sin β}$ .

Согласно теореме синусов

$\frac{x}{\sin θ} = \frac{R}{\sin φ}$ ;

отсюда следует, что

$\frac{R}{x / \sin θ} = \sin φ$ ,

т.е. выражение для вычисления T имеет вид:

$T = m g \frac{\sin φ}{\sin β}$ .

Определим углы φ и β, входящие в данное выражение.

Угол γ равен углу при основании наклонной плоскости α:

γ = α = 60°.

Из четырехугольника, противоположные углы которого γ и θ, а два остальных — прямые, найдем угол θ:

θ = 360° − 90° − 90° − γ = 180° − 60° = 120°.

Треугольник, показанный на рисунке, является равнобедренным; следовательно, угол φ определяется формулой

$φ = \frac{180 ° - θ}{2} = \frac{180 ° - 120 °}{2} = 30 °$ .

Найдем угол β:

β = 180° − 60° = 120°.

Подстановка углов φ и β в выражение для вычисления модуля силы натяжения нити дает:

$T = m g \frac{\sin 30 °}{\sin 120 °} = m g \frac{0,5}{0,5 \sqrt{3}} \frac{\sqrt{3}}{\sqrt{3}} = m g \frac{\sqrt{3}}{3}$ .

Произведем вычисление:

$T = 5,2 \cdot 10 \frac{\sqrt{3}}{3} \approx 30$ Н.