Предметы

Физика

Элементы статики и гидростатики

4.1. Элементы статики

4.1.4. Момент силы

Теория Тренинг

Физика

Общий тест

4.1. Элементы статики

4.1.4. Момент силы

Момент силы относительно некоторой точки — это векторное произведение радиус-вектора $\vec{r}$ , проведенного от этой точки к точке приложения силы, на силу $\vec{F}$ :

$\vec{M} = [\vec{r}, \vec{F}]$ .

Когда говорят о моменте силы относительно оси, проведенной через указанную точку, имеют в виду скалярную величину, равную проекции момента силы на указанную ось.

В Международной системе единиц момент силы измеряется в ньютонах, умноженных на метр (1 Н ⋅ м).

Модуль момента силы вычисляется по формуле

M = rF sin α,

где r — длина радиус-вектора, проведенного от оси вращения к точке приложения силы; F — модуль приложенной к телу силы; α — угол между векторами $\vec{r}$ и $\vec{F}$ .

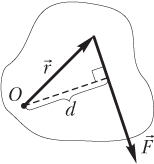
Точка O, относительно которой рассчитывается момент приложенной к телу силы $\vec{F}$ , может находиться как на самом теле (рис. 4.3), так и вне его (рис. 4.4). Радиус-вектор $\vec{r}$ проводят от точки O к точке приложения силы $\vec{F}$ .

Рис. 4.3

Рис. 4.4

На рисунках показано, как правильно определять угол α между указанными векторами в случаях их различного взаимного расположения.

Плечо силы — кратчайшее расстояние от линии действия силы (продолжение вектора силы в пространстве) до точки O (рис. 4.5).

Рис. 4.5

Плечо силы представляет собой произведение

d = r sin α,

где r — длина радиус-вектора, проведенного от оси вращения к точке приложения силы; α — угол между векторами $\vec{r}$ и $\vec{F}$ .

Модуль момента силы может быть записан в виде:

M = dF,

где d — плечо силы; F — модуль приложенной силы.

Направление момента силы определяют по правилу правого винта: направление момента $\vec{M}$ совпадает с поступательным движением правого винта, если его рукоятку вращать от $\vec{r}$ (радиус-вектор, проведенный от оси к точке приложения силы) к $\vec{F}$ (приложенная сила) по наименьшему углу.

Пример 10. Однородная лестница длиной 12 м и массой 24 кг приставлена к стене и образует с полом угол 60°. Определить момент силы тяжести относительно оси, проходящей через нижний конец лестницы параллельно ее ступенькам.

Решение. Лестница является однородной; следовательно, центр тяжести лестницы находится в ее середине.

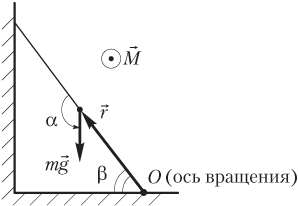
На рисунке показаны:

сила тяжести, действующая на лестницу;
радиус-вектор, проведенный от оси вращения к точке приложения силы;
угол α между указанными векторами.

Модуль момента силы тяжести относительно указанной оси определяется по формуле

M = Fr sin α,

где F = mg — модуль силы тяжести; r = l/2 — модуль радиус-вектора; l — длина лестницы; $α = (90 ° + β)$ — угол между вектором силы тяжести и радиус-вектором точки ее приложения относительно заданной оси; β — угол между лестницей и полом.

С учетом выражений для модулей силы тяжести, радиус-вектора и угла между ними формула для расчета модуля момента силы тяжести в явном виде выглядит следующим образом:

$M = m g \frac{l}{2} sin 150 °$ .

Произведем вычисление:

$M = 24 \cdot 10 \cdot \frac{12}{2} \cdot 0,5 = 0,72 \cdot 10^{3} Н \cdot м = 0,72$ кН ⋅ м.

Направление момента силы тяжести определяется по правилу правого винта: вращаем правый винт от радиус-вектора к вектору силы по наименьшему углу (против часовой стрелки); направление поступательного движения винта («к нам») совпадает с направлением данного момента; указанное направление на рисунке обозначено $⊙ \vec{M}$ .

Пример 11. Пластина в форме однородного диска площадью 314 см² закреплена на горизонтальной оси таким образом, что диаметр диска, проведенный через точку крепления, горизонтален и перпендикулярен оси вращения. Найти величину момента силы тяжести, если масса пластины составляет 300 г.

Решение. Пластина является однородной; следовательно, центр ее тяжести находится в геометрическом центре круга.

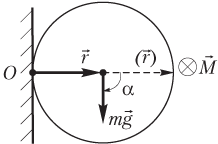
На рисунке показаны:

сила тяжести, действующая на пластину;
радиус-вектор, проведенный от оси вращения к точке приложения силы;
угол α между указанными векторами.

Модуль момента силы тяжести относительно указанной оси определяется по формуле

M = Fr sin α,

где F = mg — модуль силы тяжести; r = R — модуль радиус-вектора; R — радиус круга; α = 90° — угол между вектором силы тяжести и радиус-вектором точки ее приложения относительно заданной оси.

С учетом выражений для модулей силы тяжести, радиус-вектора и угла между ними формула для расчета модуля момента силы тяжести приобретает вид:

$M = m g R \sin 90 °$ .

Определим радиус пластины, используя выражение для площади круга:

S = πR².

Отсюда следует, что радиус круга определяется по формуле

$R = \sqrt{\frac{S}{π}}$ .

Подставим данное выражение в формулу для вычисления модуля момента силы тяжести:

$M = m g \sqrt{\frac{S}{π}} \sin 90 °$

и рассчитаем его значение:

$M = 300 \cdot 10^{- 3} \cdot 10 \sqrt{\frac{314 \cdot 10^{- 4}}{π}} \cdot 1 = 0,3 Н \cdot м = 300$ мН ⋅ м.

Направление момента силы тяжести определяется по правилу правого винта: вращаем правый винт от радиус-вектора к вектору силы по наименьшему углу (по часовой стрелке); направление поступательного движения винта («за плоскость чертежа», «от нас») совпадает с направлением данного момента; указанное направление на рисунке обозначено $\otimes \vec{M}$ .

Пример 12. Палочка в виде тонкого однородного цилиндра длиной 60 см и площадью поперечного сечения 3,0 см² закреплена на оси вращения верхним концом. Нижний конец палочки опущен в воду плотностью 1,0 г/см³ и погружен в нее на 1/3 длины. Вычислить модуль момента силы Архимеда, действующей на палочку, относительно горизонтальной оси, проходящей перпендикулярно палочке через ее верхний конец, при отклонении палочки от вертикали на 30°.

Решение. Сила Архимеда действует на погруженную в воду часть палочки и приложена к середине погруженной части.

На рисунке показаны:

сила Архимеда, действующая на погруженную в воду часть палочки;
радиус-вектор, проведенный от оси вращения к точке приложения силы;
угол α между указанными векторами.

Модуль момента силы Архимеда относительно указанной оси определяется по формуле

M = Fr sin α,

где $F = F_{A} = ρ_{0} g V^{'}$ — модуль силы Архимеда; ρ₀ — плотность воды; g — модуль ускорения свободного падения; $V^{'} = \frac{1}{3} V$ — объем погруженной части палочки; V — объем палочки; $r = \frac{5}{6} l$ — модуль радиус-вектора; l — длина палочки; $α = 180 ° - 30 ° = 150 °$ — угол между вектором силы Архимеда и радиус-вектором точки ее приложения относительно заданной оси.

С учетом выражений для модулей силы Архимеда, радиус-вектора и угла между ними формула для расчета модуля момента силы Архимеда приобретает вид:

$M = (\frac{1}{3} ρ_{0} g V) (\frac{5}{6} l) \sin 150 ° = \frac{5}{18} ρ_{0} g V l \sin 30 °$ .

Объем палочки представим в виде произведения

V = lS

и подставим в выражение для расчета модуля момента силы Архимеда:

$M = \frac{5}{18} ρ_{0} g S l^{2} \sin 30 °$ ,

где S — площадь поперечного сечения палочки.

Произведем вычисление:

$M = \frac{5}{18} \cdot 1,0 \cdot 10^{3} \cdot 10 \cdot 3,0 \cdot 10^{- 4} {(60 \cdot 10^{- 2})}^{2} \cdot 0,5 = 0,15$ Н ⋅ м.

Направление момента силы Архимеда определяется по правилу правого винта: вращаем правый винт от радиус-вектора к вектору силы по наименьшему углу (против часовой стрелки); направление поступательного движения винта («к нам») совпадает с направлением данного момента; указанное направление на рисунке обозначено $⊙ \vec{M}$ .