Физика
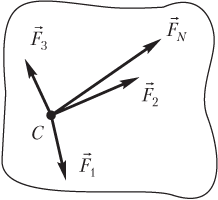
Если под действием нескольких сил тело может двигаться только поступательно, то при решении задач указанное тело можно рассматривать как материальную точку соответствующей массы, помещенную в его центр масс C (рис. 4.2).
Материальная точка, покоящаяся в некоторой инерциальной системе отсчета (ИСО), продолжает покоиться в этой ИСО, если векторная сумма всех действующих на нее сил , , ..., равна нулю:
.
Пример 4. Тетива лука в месте контакта со стрелой образует угол 90°. Найти модуль силы натяжения тетивы, если лучник тянет стрелу с силой 794 Н. Стрела расположена симметрично относительно лука.
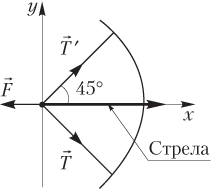
Решение. Силы, действующие на стрелу со стороны лучника и тетивы, и выбранная система координат показаны на рисунке.
Стрела находится в равновесии в том случае, когда векторная сумма сил, действующих на нее, равна нулю:
,
или в проекциях на координатные оси:
где F — модуль силы, действующей на стрелу со стороны лучника; T — модуль силы натяжения, действующей на стрелу со стороны нижней части тетивы; T′ — модуль силы натяжения, действующей на стрелу со стороны верхней части тетивы.
Натяжение тетивы лука по обе стороны от стрелы одинаково, т.е. модули сил натяжения, действующие на стрелу со стороны нижней и верхней частей тетивы, одинаковы:
T′ = T.
С учетом указанного обстоятельства система уравнений принимает вид:
а ее первое уравнение позволяет найти модуль силы натяжения тетивы:
Н.
Пример 5. Тело массой 2,7 кг висит на невесомой нерастяжимой нити. Под действием горизонтальной силы 27 Н нить отклоняется на некоторый угол от вертикали. Найти натяжение нити в новом положении равновесия.
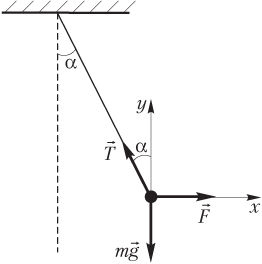
Решение. Силы, действующие на тело, и выбранная система координат показаны на рисунке.
Тело находится в равновесии в том случае, когда векторная сумма сил, действующих на него, равна нулю:
,
или в проекциях на координатные оси:
где F — модуль горизонтальной силы; T — модуль силы натяжения, действующей на тело со стороны нити; mg — модуль силы тяжести; m — масса тела; g — модуль ускорения свободного падения; α — угол отклонения нити от вертикали.
Для определения величины силы натяжения нити в новом положении равновесия исключим из системы уравнений угол, преобразовав систему следующим образом:
возведя каждое из уравнений в квадрат:
и сложив уравнения
.
Несложные преобразования с использованием равенства
sin2α + cos2α = 1
дают
.
т.е.
T2 = F2 + (mg)2.
Отсюда для вычисления величины искомой силы натяжения нити получим формулу
.
Произведем вычисление:
Н.
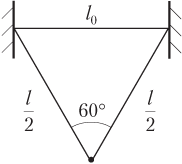
Пример 6. Невесомый эластичный шнур длиной 1,0 м подвешен за концы горизонтально и находится в нерастянутом состоянии. Когда к середине шнура подвесили груз массой 2,6 кг, длина шнура увеличилась вдвое. Найти коэффициент упругости шнура.
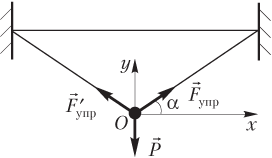
Решение. Силы, действующие на середину шнура, и выбранная система координат показаны на рисунке.
Середина шнура находится в равновесии в том случае, когда векторная сумма сил, действующих на нее, равна нулю:
,
или в проекциях на координатные оси:
где P = mg — модуль веса груза; m — масса груза; g — модуль ускорения свободного падения; Fупр — модуль силы упругости, действующей на середину шнура со стороны его правой половины; — модуль силы упругости, действующей на середину шнура со стороны его левой половины; α — угол, показанный на рисунке.
Силы упругости, действующие на середину шнура со стороны его левой и правой половин, одинаковы по величине:
,
где Fупр = k∆l — модуль силы упругости, возникающей в шнуре при его деформации, k — коэффициент упругости шнура, ∆l — деформация растяжения шнура.
С учетом указанного обстоятельства система уравнений принимает вид:
а ее второе уравнение позволяет выразить искомый коэффициент упругости:
.
Для расчета коэффициента упругости шнура по данной формуле необходимо определить:
- деформацию растяжения шнура ∆l;
- угол α, который образует шнур с осью Ox.
Для определения деформации шнура учтем, что его длина удваивается под воздействием груза (l = 2l0):
∆l = l − l0 = 2l0 − l0 = l0,
где l0 — первоначальная длина недеформированного шнура; l — длина шнура, деформированного весом подвешенного к нему груза.
Нерастянутый и растянутый шнуры образуют правильный треугольник, показанный на рисунке. Поэтому угол, который образует шнур с осью Ox, равен
α = 60°.
С учетом значений ∆l и α формула для расчета коэффициента упругости принимает вид:
,
а вычисление дает его значение:
Н/м.
Пример 7. Однородный шарик диаметром 10 мм и плотностью 8,0 г/см3 заряжен и помещен в масло плотностью 0,8 г/см3. Когда включили электростатическое поле, направленное вертикально вверх, шарик оказался взвешенным в масле. Определить напряженность электростатического поля, если заряд шарика составляет 3,4 мкКл, а диэлектрическая проницаемость масла равна 3,8.
Решение. Силы, действующие на шарик, и координатная ось показаны на рисунке.
Шарик оказывается взвешенным в масле, т.е. находится в равновесии, если векторная сумма сил, действующих на него, равна нулю:
,
или в проекции на координатную ось Oy:
Oy: mg − Fкул − FA = 0,
где Fкул = qE — модуль кулоновской силы (силы взаимодействия заряда и электростатического поля); q — заряд шарика; E — напряженность электростатического поля в масле; FA = ρ0gV — модуль силы Архимеда; ρ0 — плотность масла; g — модуль ускорения свободного падения; V — объем шарика; m = ρV — масса шарика; ρ — плотность материала, из которого изготовлен шарик.
С учетом выражений для кулоновской силы, силы Архимеда и массы шарика условие равновесия шарика приобретает вид:
qE + ρ0gV − ρVg = 0.
Выразим отсюда модуль напряженности электростатического поля в масле:
.
Однако среда (масло) уменьшает величину напряженности электростатического поля в ε раз:
,
где E0 — величина напряженности электростатического поля в вакууме; ε — диэлектрическая проницаемость среды (масла).
Таким образом, величина напряженности включенного поля в ε раз больше величины напряженности электростатического поля в масле:
.
Для вычисления величины напряженности электростатического поля необходимо выразить объем шарика через его диаметр:
,
где d — диаметр шарика.
Подставим данную формулу в выражение для расчета E0:
и произведем вычисление:
.
Пример 8. Тело массой 2,5 кг покоится на наклонной плоскости с углом при основании 45°, если на него действует прижимающая сила, равная 25 Н и направленная горизонтально. Определить модуль силы трения, действующей на данное тело со стороны наклонной плоскости.
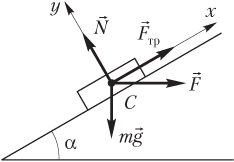
Решение. Силы, действующие на тело, и выбранная система координат показаны на рисунке.
Тело находится в равновесии в том случае, когда векторная сумма сил, действующих на него, равна нулю:
или в проекциях на координатные оси:
где F — модуль горизонтальной силы; N — модуль силы нормальной реакции опоры, действующей на тело со стороны наклонной плоскости; mg — модуль силы тяжести; m — масса тела; g — модуль ускорения свободного падения; Fтр— модуль силы трения покоя; α — угол наклона плоскости к горизонту.
Величина силы трения покоя определяется силами, которые стремятся вывести тело из положения равновесия. Модули указанных сил связаны с величиной силы трения первым уравнением системы, из которого следует, что модуль искомой силы трения определяется формулой
.
Произведем расчет:
.
Оказывается, что на тело заданной массы при указанной величине прижимающей силы сила трения не действует.
Пример 9. Брусок массой 2,7 кг удерживается на наклонной плоскости с углом при основании 60° с помощью силы, направленной вдоль наклонной плоскости. Определить минимальное значение удерживающей силы, если коэффициент трения скольжения бруска о плоскость равен 0,25.
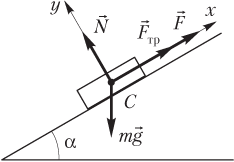
Решение. Силы, действующие на тело, и выбранная система координат показаны на рисунке.
Тело находится в равновесии в том случае, когда векторная сумма сил, действующих на него, равна нулю:
,
или в проекциях на координатные оси:
где F — модуль силы, направленной вдоль наклонной плоскости; N — модуль силы нормальной реакции опоры, действующей на тело со стороны наклонной плоскости; mg — модуль силы тяжести; m — масса тела; g — модуль ускорения свободного падения; — модуль максимальной силы трения покоя; α — угол наклона плоскости к горизонту.
Величина максимальной силы трения покоя совпадает с величиной силы трения скольжения и определяется формулой
.
Из второго уравнения системы выразим N:
N = mg cos α
и подставим в записанную формулу для максимальной силы трения покоя:
.
Подстановка данного равенства в первую формулу позволяет найти минимальное значение силы, приложенной к телу вдоль наклонной плоскости:
.
Вычислим ее величину:
Н.