Физика

Пример 3. Некоторая линейка находится в ракете и расположена под углом 60° к выбранной координатной оси. Ракета начинает удаляться от Земли с релятивистской скоростью, равной 0,60c (c — скорость света) в направлении указанной координатной оси. Найти угол поворота линейки относительно направления движения ракеты в системе отсчета, связанной Землей.

Решение. Линейка покоится относительно ракеты, поэтому собственную систему отсчета целесообразно связать с ракетой. На рис. а изображены: система координат, связанная с ракетой; линейка (ее продольный l _||0 и поперечный l _⊥0 размеры); направление скорости ракеты.

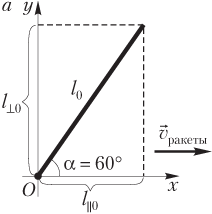
Линейка в собственной системе отсчета имеет следующие размеры:

• продольный (вдоль направления движения) —

l _||0 = l ₀ cos 60°;

• поперечный (в направлении, перпендикулярном движению):

l _⊥0 = l ₀ sin 60°,

где l ₀ — размер линейки в системе отсчета, связанной с ракетой.

В системе отсчета, связанной с Землей, линейка движется вместе с ракетой. На рис. б изображены: система координат, связанная с Землей; линейка (ее продольный l _|| и поперечный l _⊥ размеры); угол β, который образует линейка с направлением движения ракеты в системе отсчета, связанной с Землей.

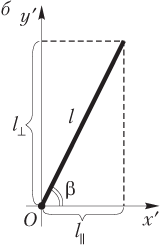
Линейка в указанной системе отсчета имеет следующие размеры:

• продольный —

$l_{\left|\right|}=l_{\left|\right|0}\sqrt{1-\frac{v^2}{c^2}}$;

• поперечный —

l _⊥ = l _⊥0,

где v — модуль скорости ракеты, v = 0,6 с; c — скорость света в вакууме.

Продольный размер линейки уменьшается, а поперечный остается неизменным.

Угол, который составляет линейка с координатной осью Ox′, определяется формулой

$\mathrm{tg}\beta =\frac{l_{\perp }}{l_{\left|\right|}}=\frac{l_{\left|\right|0}\sqrt{1-\frac{v^2}{c^2}}}{l_{\perp 0}}=\frac{l_0\cos 60°\sqrt{1-\frac{v^2}{c^2}}}{l_0\sin 60°}=\frac{\sqrt{1-\frac{v^2}{c^2}}}{\mathrm{tg}60°}=\frac{\sqrt{3}}{3}\sqrt{1-\frac{v^2}{c^2}}$.

Расчет дает значение угла β:

β = arctg(2,165) = 65°.

Угол поворота линейки относительно направления движения ракеты в системе отсчета, связанной с Землей, составляет

γ = β − α = 65° − 60° = 5°.

Пример 4. Из материала, имеющего в земных условиях плотность 7,80 г/см³, изготовлен стержень и помещен в ракету. Ракета движется со скоростью 0,70c (c — скорость света), а стержень расположен в ракете вдоль направления ее движения. Найти увеличение плотности материала стержня по расчетам земного наблюдателя.

Решение. Стержень покоится относительно ракеты, поэтому собственную систему отсчета целесообразно связать с ракетой. На рис. а изображены: система координат, связанная с ракетой; стержень (его длина l ₀ и площадь поперечного сечения S); направление скорости ракеты.

Стержень в указанной системе отсчета имеет массу m ₀ и плотность

${\rho }_0=\frac{m_0}{V_0}=\frac{m_0}{l_{0}S}$,

где V ₀ — объем стержня в собственной системе отсчета, V ₀ = l ₀S.

В системе отсчета, связанной с Землей, стержень движется вместе с ракетой. На рис. б изображены: система координат, связанная с Землей; стержень (его длина l и площадь поперечного сечения S).

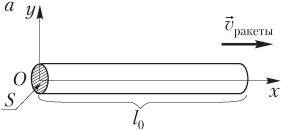
Стержень в указанной системе отсчета имеет массу m и плотность

$\rho =\frac{m}{V}=\frac{m}{lS}$,

где V — объем стержня в системе отсчета, связанной с Землей, V = lS.

Площадь поперечного сечения стержня в обеих системах отсчета одинакова.

Отношение плотностей

$\frac{\rho }{{\rho }_0}=\frac{m{l}_{0}S}{m_{0}lS}=\frac{m{l}_0}{m_{0}l}$

дает выражение для плотности стержня в системе отсчета, связанной с Землей:

$\rho =\frac{{\rho }_{0}m{l}_0}{m_{0}l}$.

Продольный размер стержня для земного наблюдателя уменьшается:

$l=l_0\sqrt{1-\frac{v^2}{c^2}}$,

а масса стержня увеличивается:

$m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$,

где v — скорость ракеты, v = 0,70c; c — скорость света в вакууме.

Подстановка m, l и v в выражение для плотности дает формулу

$\rho =\frac{{\rho }_0{l}_0}{m_0{l}_0\sqrt{1-\frac{v^2}{c^2}}}\cdot \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{{\rho }_0}{1-\frac{v^2}{c^2}}=\frac{{\rho }_0}{1-\frac{{\left(\mathrm{0,7}c\right)}^2}{c^2}}=\frac{{\rho }_0}{\mathrm{0,51}}$.

Искомое изменение плотности:

$\Delta \rho =\rho -{\rho }_0={\rho }_0\left(\frac{1}{\mathrm{0,51}}-1\right)=\frac{49}{51}{\rho }_0$.

Вычислим:

$\Delta \rho =\frac{49\cdot \mathrm{7,8}\cdot {10}^3}{51}=\mathrm{7,5}\cdot {10}^3{\text{ кг/м}}^3=\mathrm{7,5}{\text{ г/см}}^3$.

Плотность материала, из которого изготовлен стержень, относительно земного наблюдателя увеличивается на 7,5 г/см³.

Пример 5. Часы помещены в ракету, удаляющуюся от Земли с релятивистской скоростью 0,80c (c — скорость света). Найти разницу показаний часов на Земле и в ракете, если по ракетным часам проходит 10,0 сут.

Решение. Часы покоятся относительно ракеты, поэтому собственную систему отсчета целесообразно связать с ракетой.

По часам, расположенным в собственной системе отсчета (ракете), проходит промежуток времени τ₀ = 10 сут.

В системе отсчета, связанной с Землей, проходит промежуток времени, который определяется формулой

$\tau =\frac{{\tau }_0}{\sqrt{1-\frac{v^2}{c^2}}}$,

где v — скорость ракеты, v = 0,80c; c — скорость света в вакууме.

Искомая разница в показаниях часов определяется разностью

$\Delta \tau =\tau -{\tau }_0={\tau }_0\left(\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}-1\right)$

и составляет

$\Delta \tau =10\cdot 24\cdot \left(\frac{1}{\sqrt{1-\frac{{\left(\mathrm{0,8}c\right)}^2}{c^2}}}-1\right)=\frac{10\cdot 24\cdot \mathrm{0,4}}{\mathrm{0,6}}=160$ ч.

На Земле пройдет на 160 ч больше, чем в ракете.