Репетитор-онлайн — подготовка к ЦТ

5.4. Практическое применение уравнения состояния идеального газа

5.4.4. Уравнение состояния для газа в трубке

Уравнение состояния для газа в горизонтальной запаянной трубке

Если идеальный газ находится в горизонтальной запаянной трубке (горизонтальном закрытом сосуде) и разделен на две части легкоподвижной перегородкой, то уравнение состояния следует записывать для левой и правой частей трубки по отдельности.

Для идеального газа (газов), находящегося в горизонтальной запаянной трубке, разделенной легкоподвижной перегородкой:

давление газа (газов) в обеих частях трубки одинаково в тот момент, когда перегородка неподвижна:

p ₁ = p ₂ = p = const;

остальные параметры газа (газов) могут отличаться.

Пусть слева и справа от перегородки (рис. 5.10) находятся разные идеальные газы при разной температуре. В тот момент, когда перегородка покоится, уравнения Менделеева — Клапейрона записываются для них в виде системы:

Рис. 5.10

$\begin{array}{l} p V_{1} = ν_{1} R T_{1}, \\ p V_{2} = ν_{2} R T_{2}, \end{array}}$

где p, V ₁, ν₁, T ₁ — давление, объем, количество вещества и температура газа, находящегося в левой части трубки; p, V ₂, ν₂, T ₂ — давление, объем, количество вещества и температура газа, находящегося в правой части трубки; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).

Уравнение состояния для газа в вертикальной запаянной трубке

Если идеальный газ находится в вертикальной запаянной трубке и разделен на две части легкоподвижной перегородкой, то уравнение состояния следует записывать для верхней и нижней частей трубки, дополняя систему выражением для давления, которое оказывает перегородка на нижнюю часть газа.

Для идеального газа (газов), находящегося в вертикальной запаянной трубке, разделенной горизонтальной легкоподвижной перегородкой:

давление газа (газов) в верхней и нижней частях трубки различно

p ₁ ≠ p ₂;

остальные параметры газа (газов) также могут отличаться.

Давления газа в верхней и нижней частях трубки связаны между собой соотношением

p ₂ = p ₁ + p ₀,

где p ₂ — давление газа в нижней части трубки; p ₁ — давление газа в верхней части трубки; p ₀ — давление перегородки на газ, находящийся в нижней части трубки.

Пусть сверху и снизу от перегородки (рис. 5.11) находится идеальный газ при разной температуре; тогда уравнения Менделеева — Клапейрона записываются для него в виде системы:

Рис. 5.11

$\begin{array}{l} p_{1} V_{1} = ν_{1} R T_{1}, \\ p_{2} V_{2} = ν_{2} R T_{2}, \end{array}}$

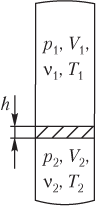
где p ₁, V ₁, ν₁, T ₁ — давление, объем, количество вещества и температура газа, находящегося в верхней части трубки; p ₂, V ₂, ν₂, T ₂ — давление, объем, количество вещества (газа) и температура газа, находящегося в нижней части трубки; R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К).

Давление перегородки на газ, находящийся в нижней части запаянной вертикальной трубки, может рассчитываться по двум различным формулам:

$p_{0} = \frac{m g}{S}$ или p ₀ = ρgh,

где m — масса перегородки; g — модуль ускорения свободного падения; S — площадь сечения трубки; ρ — плотность вещества перегородки (используется в том случае, когда перегородкой является столбик жидкости высотой h).

Уравнение состояния для газа в трубке, запаянной с одной стороны

Если идеальный газ находится в вертикальной, открытой с одного конца трубке и отделен от атмосферы легкоподвижной перегородкой, находящейся в равновесии, то существует соотношение, связывающее давление газа с атмосферным. Вид формулы зависит от того, какой из концов трубки является открытым.

Пусть идеальный газ находится в нижней части вертикальной трубки с открытым верхним концом и отделен от атмосферы легкоподвижной перегородкой (рис. 5.12).

Рис. 5.12

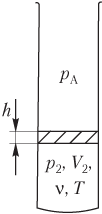
Тогда давление газа в трубке связано с атмосферным давлением формулой

p _A + p ₀ = p ₂,

где p _A — атмосферное давление; p ₂ — давление газа в нижней части трубки; р ₀ — давление перегородки на газ, находящийся в нижней части трубки, рассчитывается по одной из формул:

$p_{0} = \frac{m g}{S}$ или p ₀ = ρgh,

где m — масса перегородки; g — модуль ускорения свободного падения; S — площадь сечения трубки; ρ — плотность вещества перегородки; h — высота перегородки.

Уравнение Менделеева — Клапейрона записывается только для газа, находящегося в нижней части трубки:

p ₂V ₂ = νRT,

где V ₂ — объем, занимаемый газом; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T — температура газа.

Пусть идеальный газ находится в верхней части вертикальной трубки с открытым нижним концом и отделен от атмосферы легкоподвижной перегородкой (рис. 5.13). Тогда давление газа в трубке связано с атмосферным давлением формулой

Рис. 5.13

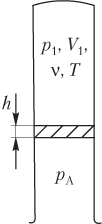
p ₁ + p ₀ = p _A,

где p ₁ — давление газа в верхней части трубки; p _A — атмосферное давление; p ₀ — давление перегородки на столб воздуха, находящегося снаружи трубки, рассчитывается по одной из формул

$p_{0} = \frac{m g}{S}$ или p ₀ = ρgh.

Уравнение Менделеева — Клапейрона записывается только для газа, находящегося в верхней части трубки:

p ₁V ₁ = νRT,

где V ₁ — объем, занимаемый газом; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); T — температура газа.

Пример 22. Закрытый цилиндр длиной 110 см, расположенный горизонтально, разделен легкоподвижным поршнем на две равные части. В обеих частях цилиндра находится один и тот же газ при температуре 300 К. На сколько градусов нужно нагреть газ в одной из частей цилиндра для того, чтобы поршень сместился на 50 мм?

Решение. Количество газа ν в левой и правой частях цилиндра одинаково. Рисунок иллюстрирует условие задачи:

поршень находится посередине цилиндра (рис. а) — газ в обеих частях цилиндра характеризуется параметрами p ₁, V, T ₁; давление газа по обе стороны от поршня одинаково: p ₁ = const;

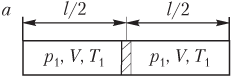
поршень смещается влево при повышении температуры газа в правой части цилиндра (рис. б) — газ слева от поршня характеризуется параметрами p ₂, V ₁, T ₁, а справа — параметрами p ₂, V ₂, T ₂; давление газа по обе стороны от поршня также одинаково: p ₂ = const.

Запишем уравнение Менделеева — Клапейрона для трех состояний газа, показанных на рисунке:

$\begin{array}{l} p_{1} V = ν R T_{1}, \\ p_{2} V_{1} = ν R T_{1}, \\ p_{2} V_{2} = ν R T_{2}, \end{array}}$

где V, V ₁,V ₂ — объемы газа в указанных состояниях, V = Sl/2, V ₁ = Sl ₁, V ₂ = Sl ₂; S — площадь поперечного сечения сосуда; l/2, l ₁, l ₂ — расстояния, показанные на рисунке; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).

Искомой величиной является разность температур:

ΔT = T ₂ − T ₁,

определяемая разностью третьего и второго уравнений:

p ₂(V ₂ − V ₁) = νR(T ₂ − T ₁).

Деление записанного уравнения на первое уравнение системы дает

$\frac{p_{2} (V_{2} - V_{1})}{p_{1} V} = \frac{ν R (T_{2} - T_{1})}{ν R T_{1}}$ ,

а с учетом явного вида объемов искомая разность температур определяется формулой

$Δ T = \frac{p_{2} T_{1}}{p_{1}} \cdot \frac{(V_{2} - V_{1})}{V} = \frac{p_{2} T_{1}}{p_{1}} \cdot \frac{l_{2} - l_{1}}{l / 2}$ .

Отношение давлений найдем делением первых двух уравнений системы:

$\frac{p_{2} V_{1}}{p_{1} V} = \frac{ν R T_{1}}{ν R T_{1}} = 1$ , т.е. $\frac{p_{2}}{p_{1}} = \frac{V}{V_{1}} = \frac{l / 2}{l_{1}}$ .

Подстановка в выражение для разности температур дает

$Δ T = T_{1} \cdot \frac{l / 2}{l_{1}} \cdot \frac{l_{2} - l_{1}}{l / 2} = T_{1} \cdot \frac{l_{2} - l_{1}}{l_{1}} = T_{1} \cdot (\frac{l_{2}}{l_{1}} - 1)$ .

Расстояния, входящие в формулу, определяются следующим образом:

$\begin{matrix} l_{1} = l / 2 - Δ l, \\ l_{2} = l / 2 + Δ l, \end{matrix}}$

где ∆l — смещение поршня.

Тогда искомая разность температур определяется формулой

$Δ T = T_{1} \cdot (\frac{l / 2 + Δ l}{l / 2 - Δ l} - 1)$

и составляет

$Δ T = 300 \cdot (\frac{110 \cdot 10^{- 2} / 2 + 50 \cdot 10^{- 3}}{110 \cdot 10^{- 2} / 2 - 50 \cdot 10^{- 3}} - 1) = 60 К = 60$ °С.

Нагревание газа в правой части цилиндра на 60 °С приводит к смещению поршня влево на указанное расстояние.

Пример 23. Найти давление газа в горизонтальной запаянной трубке сечением 50 мм², разделенной столбиком ртути массой 12 г на два объема по 60 см³, если при повороте трубки в вертикальное положение нижний объем равен 30 см³. Температура газа при повороте трубки не изменяется.

Решение. Количество газа ν в обеих частях трубки одинаково. Рисунок иллюстрирует условие задачи:

столбик ртути находится посередине трубки (рис. а) — газ в обеих частях трубки характеризуется параметрами p, V, T; давление газа по обе стороны от столбика ртути одинаково: p = const;

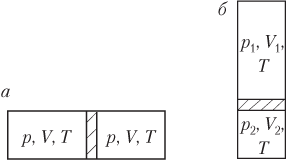
столбик ртути смещается вниз при повороте трубки в вертикальное положение (рис. б) — газ в верхней части трубки характеризуется параметрами p ₁, V ₁, T, а в нижней части трубки — параметрами p ₂, V ₂, T; давления газа в верхней и нижней части трубки связаны соотношением

p ₂ = p ₁ + p ₀,

где p ₀ — давление столбика ртути на газ, находящийся в нижней части трубки —

$p_{0} = \frac{m g}{S}$ ,

где m — масса столбика ртути; g — ускорение свободного падения; S — площадь поперечного сечения сосуда;

Запишем уравнение Менделеева — Клапейрона для трех состояний газа, показанных на рисунке:

$\begin{array}{l} p V = ν R T, \\ p_{1} V_{1} = ν R T, \\ p_{2} V_{2} = ν R T, \end{array}}$

где R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).

Деление первого уравнения на второе позволяет выразить давление газа в верхней части трубки через давление газа в трубке, находящейся в горизонтальном положении:

$\frac{p V}{p_{1} V_{1}} = \frac{ν R T}{ν R T}$ , т.е. $p_{1} = p \frac{V}{V_{1}}$ .

Делением первого уравнения на третье выразим давление газа в нижней части трубки через давление газа в трубке, находящейся в горизонтальном положении:

$\frac{p V}{p_{2} V_{2}} = \frac{ν R T}{ν R T}$ , т.е. $p_{2} = p \frac{V}{V_{2}}$ .

Подстановка полученных выражений в формулу, связывающую давления газа в верхней и нижней частях трубки, дает

$p \frac{V}{V_{2}} = p \frac{V}{V_{1}} + p_{0}$ , или $p = p_{0} \frac{V_{1} V_{2}}{V (V_{1} - V_{2})}$ .

Найдем объем V ₁, считая объемы V и V ₂ известными:

V = 60 см³, V ₂ = 30 см³.

Из равенства

2V = V ₁ + V ₂

следует, что

V ₁ = 2V − V ₂ = 2 ⋅ 60 − 30 = 90 см³.

Давление газа в горизонтальной трубке определяется формулой

$p = p_{0} \frac{90 \cdot 30}{60 \cdot (90 - 30)} = 0,75 p_{0} = 0,75 \frac{m g}{S}$ .

Произведем вычисление:

$p = 0,75 \cdot \frac{12 \cdot 10^{- 3} \cdot 10}{50 \cdot 10^{- 6}} = 1,8 \cdot 10^{3} Па = 1,8$ кПа.

Следовательно, давление газа в горизонтальной трубке было равно 1,8 кПа.

Пример 24. Газ, находящийся в горизонтальной трубке, запаянной с одного конца, заперт столбиком ртути плотностью 13,6 г/см³. Объем газа составляет 240 см³, а длина столбика ртути — 150 мм. При повороте трубки в вертикальное положение открытым концом вверх, объем газа становится равным 200 см³. Найти атмосферное давление.

Решение. Рисунок иллюстрирует условие задачи:

трубка расположена горизонтально (рис. а) — давление газа p ₁ равно атмосферному давлению p _A:

p ₁ = p _A,

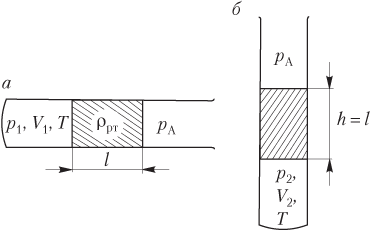
объем газа, запертого столбиком ртути, равен значению, указанному в условии задачи:

V ₁ = 240 см³;

трубка расположена вертикально (открытым концом вверх) (рис. б) — давление газа в нижней части равно сумме давлений:

p ₂ = p _A + ρ_ртgh,

где ρ_рт — плотность ртути; g — модуль ускорения свободного падения; h — длина столбика ртути, h = l;

объем газа в нижней части трубки

V ₂ = 200 см³;

количество газа и его температура при повороте трубки не изменяются:

ν = const, T = const.

Запишем уравнения Менделеева — Клапейрона для двух состояний газа в следующем виде:

трубка расположена горизонтально —

p ₁V ₁ = νRT,

где p ₁, V ₁ — давление и объем газа, запертого столбиком ртути, при горизонтальном положении трубки; ν — количество газа, запертого столбиком ртути; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);

трубка расположена вертикально —

p ₂V ₂ = νRT,

где p ₂, V ₂ — давление и объем газа, запертого столбиком ртути, при вертикальном положении трубки.

Равенство правых частей уравнений состояния газа позволяет записать:

p ₁V ₁ = p ₂V ₂,

или, в явном виде, —

p _AV ₁ = (p _A + ρ_ртgh)V ₂.

Отсюда следует, что искомое атмосферное давление определяется формулой

$p_{A} = \frac{ρ_{рт} g h V_{2}}{V_{1} - V_{2}}$ .

Расчет дает величину

$p_{A} = \frac{13,6 \cdot 10^{3} \cdot 10 \cdot 150 \cdot 10^{- 3} \cdot 200 \cdot 10^{- 6}}{240 \cdot 10^{- 6} - 200 \cdot 10^{- 6}} = 102 \cdot 10^{3} Па = 102$ кПа.

Следовательно, атмосферное давление составляет 102 кПа.

Пример 25. Газ, находящийся в горизонтальной трубке, запаянной с одного конца, заперт столбиком ртути плотностью 13,6 г/см³. Объем газа составляет 208 см³, а длина столбика ртути — 150 мм. При повороте трубки в вертикальное положение открытым концом вниз, объем газа становится равным 260 см³. Найти атмосферное давление.

Решение. Рисунок иллюстрирует условие задачи:

трубка расположена горизонтально (а) — давление газа p ₁ равно атмосферному давлению p _A ^:

p ₁ = p _A,

объем газа, запертого столбиком ртути, равен значению, указанному в условии задачи:

V ₁ = 208 см³;

трубка расположена вертикально (открытым концом вниз) (б) — давление газа в нижней части равно сумме давлений:

p _A = p ₂ + ρ_ртgh,

где ρ_рт — плотность ртути; g — модуль ускорения свободного падения; h — длина столбика ртути, h = l;

объем газа в нижней части трубки:

V ₂ = 260 см³;

количество газа и его температура при повороте трубки не изменяются:

ν = const, T = const.

Запишем уравнения Менделеева — Клапейрона для двух состояний газа в следующем виде:

трубка расположена горизонтально —

p ₁V ₁ = νRT,

трубка расположена вертикально —

p ₂V ₂ = νRT,

где R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К)

Равенство правых частей уравнений состояния газа позволяет записать:

p ₁V ₁ = p ₂V ₂,

или, в явном виде, —

p _AV ₁ = (p _A − ρ_ртgh)V ₂.

Отсюда следует, что искомое атмосферное давление определяется формулой

$p_{A} = \frac{ρ_{рт} g h V_{2}}{V_{2} - V_{1}}$ .

Расчет дает величину

$p_{A} = \frac{13,6 \cdot 10^{3} \cdot 10 \cdot 150 \cdot 10^{- 3} \cdot 260 \cdot 10^{- 6}}{260 \cdot 10^{- 6} - 208 \cdot 10^{- 6}} = 102 \cdot 10^{3} Па = 102$ кПа.

Следовательно, атмосферное давление составляет 102 кПа.

Физика