Репетитор-онлайн — подготовка к ЦТ

5.4. Практическое применение уравнения состояния идеального газа

5.4.1. Уравнение состояния для идеального газа в открытом сосуде

При рассмотрении идеального газа, находящегося в открытом сосуде, необходимо учитывать, что вследствие изменения термодинамических параметров часть газа выходит из сосуда. При этом уравнение состояния записывается только для той части газа, которая остается в сосуде.

Для идеального газа, находящегося в открытом сосуде, необходимо учитывать следующее:

масса газа изменяется в результате изменения его термодинамических параметров:

m ≠ const;

рассматривается газ, оставшийся в сосуде определенного объема, т.е. объем газа фиксирован:

V = const;

давление газа может изменяться или оставаться постоянным (в зависимости от условия задачи), причем на изменение давления в условии задачи обычно бывает четкое указание.

Если давление идеального газа в открытом сосуде по условию задачи изменяется (p ≠ const), то уравнение Менделеева — Клапейрона записывается для двух состояний газа в виде системы (рис. 5.7):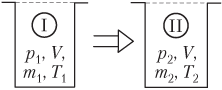Рис. 5.7

$\begin{array}{l} p_{1} V = \frac{m_{1}}{M} R T_{1}, \\ p_{2} V = \frac{m_{2}}{M} R T_{2}, \end{array}}$

где p ₁, m ₁, T ₁ — давление, масса и температура газа в начальном состоянии; p ₂, m ₂, T ₂ — указанные параметры газа в конечном состоянии; V — объем сосуда; M — молярная масса газа; R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К).

Если давление идеального газа в открытом сосуде по условию задачи остается постоянным (p = const), то изменения некоторых характеристик газа в открытом сосуде можно вычислить по следующим формулам:

изменение массы

$Δ m = m_{1} - m_{2} = m_{1} (1 - \frac{T_{1}}{T_{2}})$ ,

где m ₁ — первоначальная масса газа; m ₂ — масса газа в конце процесса; T ₁ — термодинамическая (абсолютная) температура газа в начале процесса; T ₂ — термодинамическая (абсолютная) температура газа в конце процесса;

изменение плотности

$Δ ρ = ρ_{1} - ρ_{2} = ρ_{1} (1 - \frac{T_{1}}{T_{2}})$ ,

где ρ₁ — первоначальная плотность газа; ρ₂ — плотность газа в конце процесса;

изменение количества вещества

$Δ ν = ν_{1} - ν_{2} = ν_{1} (1 - \frac{T_{1}}{T_{2}})$ ,

где ν₁ — первоначальное количество вещества (газа) в сосуде; ν₂ — количество вещества (газа) в сосуде в конце процесса.

Пример 11. В открытом сосуде объемом 450 дм³ содержится некоторое количество идеального газа. Температуру газа увеличивают от 27 до 177 °С. Давление газа остается постоянным и равным 166 кПа. Сколько моль газа выйдет из сосуда?

Решение. Запишем уравнение Менделеева — Клапейрона для двух состояний газа, находящегося в открытом сосуде, при нагревании:

для начального состояния

pV = ν₁RT ₁;

для конечного состояния

pV = ν₂RT ₂;

где p — давление газа, p = const; V — объем газа (сосуда), V = const; ν₁, ν₂ — количество вещества (газа) в начале и в конце процесса; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T ₁, T ₂ — температура газа в начале и в конце процесса.

Первое уравнение позволяет получить формулу для расчета количества вещества (газа) в начале процесса:

$ν_{1} = \frac{p V}{R T_{1}}$ .

Подстановка полученной формулы в уравнение

$Δ ν = ν_{1} (1 - \frac{T_{1}}{T_{2}})$

дает искомую разность

$Δ ν = \frac{p V}{R T_{1}} (1 - \frac{T_{1}}{T_{2}}) = \frac{p V (T_{2} - T_{1})}{R T_{1} T_{2}}$ .

Для вычисления искомой величины необходимо перевести температуру из градусов Цельсия в кельвины:

T ₁ = t ₁ + 273 = 27 + 273 = 300 К,

T ₂ = t ₂ + 273 = 177 + 273 = 450 К.

Произведем вычисление:

$Δ ν = \frac{166 \cdot 10^{3} \cdot 450 \cdot 10^{- 3} (450 - 300)}{8,31 \cdot 450 \cdot 300} = 10$ моль.

При нагревании из сосуда вышло 10 моль газа.

Пример 12. В баллоне при температуре 15 °С находится идеальный газ. Из баллона выходит 40 % газа, а температура при этом понижается на 8,0 °С. Во сколько раз уменьшится давление газа в баллоне?

Решение. Запишем уравнение Менделеева — Клапейрона для двух состояний газа, находящегося в открытом сосуде:

для начального состояния

p ₁V = ν₁RT ₁;

для конечного состояния

p ₂V = ν₂RT ₂;

где p ₁ — давление газа в начальном состоянии; p ₂ — давление газа в конечном состоянии; V — объем газа (сосуда), V = const; ν₁, ν₂ — количество вещества (газа) в начале и в конце процесса соответственно; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T ₁, T ₂ — температура газа в начале и в конце процесса соответственно.

Искомой величиной является отношение давлений p ₁/p ₂, которое определим из отношения уравнений:

$\frac{p_{1} V}{p_{2} V} = \frac{ν_{1} R T_{1}}{ν_{2} R T_{2}}$ , т.е. $\frac{p_{1}}{p_{2}} = \frac{ν_{1} T_{1}}{ν_{2} T_{2}}$ .

В результате процесса из баллона выходит 40 % газа, поэтому количество вещества (газа) ν₂, оставшегося в баллоне, составляет 60 % от количества вещества (газа) ν₁, которое было в начале процесса:

ν₂ = 0,6ν₁.

Для вычисления искомой величины необходимо сделать перевод температуры, заданной в градусах Цельсия, в кельвины:

T ₁ = t ₁ + 273 = 15 + 273 = 288 К,

T ₂ = t ₂ + 273 = (t ₁ − Δt) + 273 = (15 − 8,0) + 273 = 280 К.

Подстановка температур и количества вещества (газа), оставшегося в баллоне, в выражение для искомой величины дает

$\frac{p_{1}}{p_{2}} = \frac{ν_{1} T_{1}}{0,6 ν_{1} T_{2}} = \frac{T_{1}}{0,6 T_{2}} = \frac{288}{0,6 \cdot 280} = 1,7$ .

Давление газа в баллоне понизится в 1,7 раза.

Физика