Репетитор-онлайн — подготовка к ЦТ

5.3. Уравнение состояния идеального газа для изопроцессов

5.3.1. Изопроцессы в идеальном газе

Процессы, происходящие с определенной массой идеального газа при фиксированном термодинамическом параметре, называются изопроцессами.

При рассмотрении всех изопроцессов (изотермического, изобарного, изохорного) массу идеального газа считают неизменной величиной, т.е.

m = const.

При изотермическом процессе температура фиксированной массы идеального газа (m = const) не изменяется (T = const), тогда произведение давления на объем остается постоянной величиной:

pV = const

— закон Бойля — Мариотта (рис. 5.1).

Рис. 5.1

При решении задач уравнение Менделеева — Клапейрона записывают для двух состояний идеального газа в виде следующей системы:

$\begin{array}{l} p_{1} V_{1} = ν R T, \\ p_{2} V_{2} = ν R T, \end{array}}$

где p ₁, V ₁ — давление и объем газа в начальном состоянии; p ₂, V ₂ — давление и объем газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); Т — температура газа.

Из системы следует, что

p ₁V ₁ = p ₂V ₂.

При изобарном процессе давление фиксированной массы идеального газа (m = const) не изменяется (p = const), тогда отношение объема к температуре остается постоянной величиной:

$\frac{V}{T} = const$

— закон Гей — Люссака (рис. 5.2).

Рис. 5.2

При решении задач уравнение Менделеева — Клапейрона записывают для двух состояний идеального газа в виде следующей системы:

$\begin{array}{l} p V_{1} = ν R T_{1}, \\ p V_{2} = ν R T_{2}, \end{array}}$

где T ₁, V ₁ — температура и объем газа в начальном состоянии; T ₂, V ₂ — температура и объем газа в конечном состоянии.

Из системы следует, что

$\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}$ .

При изохорном процессе объем фиксированной массы идеального газа (m = const) не изменяется (V = const), тогда отношение давления к температуре остается постоянной величиной:

$\frac{p}{T} = const$

— закон Шарля (рис. 5.3).

Рис. 5.3

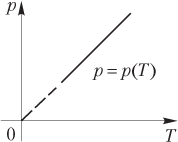
При решении задач уравнение Менделеева — Клапейрона записывают для двух состояний идеального газа в виде следующей системы:

$\begin{array}{l} p_{1} V = ν R T_{1}, \\ p_{2} V = ν R T_{2} . \end{array}}$

где p ₁, T ₁ — давление и температура газа в начальном состоянии; p ₂, T ₂ — давление и температура газа в конечном состоянии.

Из системы следует, что

$\frac{p_{1}}{T_{1}} = \frac{p_{2}}{T_{2}}$ .

Пример 8. На сколько процентов следует уменьшить объем идеального газа при изотермическом процессе для того, чтобы его давление возросло в 1,60 раза?

Решение. Искомой величиной является отношение

$η = \frac{Δ V}{V_{1}} \cdot 100 %$ ,

где ΔV = V ₁ − V ₂ — абсолютное уменьшение объема при увеличении давления; V ₁ — объем газа при давлении p ₁; V ₂ — объем газа при давлении p ₂.

Преобразуем отношение следующим образом:

$η = \frac{V_{1} - V_{2}}{V_{1}} \cdot 100 % = (1 - \frac{V_{2}}{V_{1}}) \cdot 100 %$ .

Для определения отношения объемов дважды запишем уравнение Менделеева — Клапейрона для состояния идеального газа при изотермическом процессе:

для начального состояния

p ₁V ₁ = νRT;

для конечного состояния

p ₂V ₂ = νRT,

где ν — количество вещества (газа); T — температура газа; R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); при записи уравнения состояния газа индекс у температуры не ставим, так как процесс является изотермическим (T = const).

Из системы

$\begin{array}{l} p_{1} V_{1} = ν R T, \\ p_{2} V_{2} = ν R T \end{array}}$

следует равенство

p ₁V ₁ = p ₂V ₂.

Подставив отношение объемов

$\frac{V_{2}}{V_{1}} = \frac{p_{1}}{p_{2}}$

в выражение для η, получим искомую величину:

$η = (1 - \frac{p_{1}}{p_{2}}) \cdot 100 % = (1 - \frac{p_{1}}{1,6 p_{1}}) \cdot 100 % = 37,5 %$ .

Таким образом, для увеличения давления в 1,60 раза при изотермическом процессе объем газа следует уменьшить на 37,5 %.

Пример 9. Идеальный газ находится при температуре 300 К. Сначала изобарически увеличивают в 2 раза объем газа, а затем — изохорически уменьшают в 2 раза его давление. Определить разность температур начального и конечного состояния газа.

Решение. Состояния, которые проходит газ в результате указанных процессов, схематично покажем на рисунке; параметры, не изменяющиеся при переходе из одного состояния в другое, обозначим одинаковыми индексами.

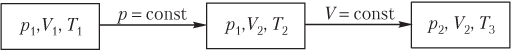
Переход газа из начального состояния в конечное осуществляется в два этапа и описывается парами уравнений:

1) из начального состояния в промежуточное (изобарный процесс) —

$\begin{array}{l} p_{1} V_{1} = ν R T_{1}, \\ p_{1} V_{2} = ν R T_{2}, \end{array}}$

где p ₁ — давление (постоянное), p ₁ = const; V ₁ — объем газа в начальном состоянии; ν — количество вещества (постоянная величина, так как изменение состояния газа происходит в результате изопроцессов); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T ₁ — температура газа в начальном состоянии; V ₂ — объем газа в промежуточном состоянии; T ₂ — температура газа в промежуточном состоянии;

2) из промежуточного состояния в конечное (изохорный процесс) —

$\begin{array}{l} p_{1} V_{2} = ν R T_{2}, \\ p_{2} V_{2} = ν R T_{3}, \end{array}}$

где V ₂ — объем (постоянный), V ₂ = const; p ₂ — давление газа в конечном состоянии; T ₃ — температура газа в конечном состоянии.

Записанные уравнения состояния образуют систему

$\begin{array}{l} p_{1} V_{1} = ν R T_{1}, \\ p_{1} V_{2} = ν R T_{2}, \\ p_{2} V_{2} = ν R T_{3}, \end{array}}$

из которой следует найти температуру конечного состояния газа T ₃ и рассчитать разность

ΔT = T ₃ − T ₁.

Для определения температуры T ₃ разделим третье уравнение системы на первое

$\frac{p_{2} V_{2}}{p_{1} V_{1}} = \frac{ν R T_{3}}{ν R T_{1}}$

и выразим искомую температуру

$T_{3} = T_{1} \frac{p_{2} V_{2}}{p_{1} V_{1}}$ .

С учетом заданного в условии отношения объемов (V ₂ = 2V ₁) и давлений (p ₁ = 2p ₂) имеем:

$T_{3} = T_{1} \frac{p_{2} \cdot 2 V_{1}}{2 p_{2} \cdot V_{1}} = T_{1}$ .

Тогда искомая разность температур

ΔT = T ₃ − T ₁ = 0,

т.е. в результате указанных процессов температура газа не изменится.

Пример 10. При изотермическом сжатии объем идеального газа уменьшают на 1,0 л, а давление газа при этом возрастает на 20 %. Затем первоначальный объем газа уменьшают на 2,0 л. На сколько процентов при этом увеличивается давление газа?

Решение. Состояния, которые проходит газ в результате двух изотермических процессов, схематично покажем на рисунке, где а, б — первый и второй процессы соответственно.

Параметры, не изменяющиеся при переходе газа из одного состояния в другое, обозначим одинаковыми индексами.

Давление газа при изотермическом сжатии изменяется:

в первом процессе на

$η_{1} = \frac{p_{2} - p_{1}}{p_{1}} \cdot 100 % = (\frac{p_{2}}{p_{1}} - 1) \cdot 100 % = 20 %$ ;

во втором процессе на

$η_{2} = \frac{p_{3} - p_{1}}{p_{1}} \cdot 100 % = (\frac{p_{3}}{p_{1}} - 1) \cdot 100 %$ ,

где p ₁ — первоначальное давление газа; p ₂ — конечное состояние газа в первом процессе; p ₃ — конечное состояние газа во втором процессе.

Искомой величиной является η₂; задача сводится к определению отношения p ₃/p ₁.

Переход газа из начального состояния в конечное в двух изотермических процессах описывается парами уравнений:

для первого процесса

$\begin{array}{l} p_{1} V_{1} = ν R T, \\ p_{2} V_{2} = ν R T, \end{array}}$

где p ₁ — давление газа в начальном состоянии; V ₁ — объем газа в начальном состоянии; ν — количество вещества (постоянная величина); p ₂ — давление газа в конечном состоянии; V ₂ — объем газа в конечном состоянии; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа.

для второго процесса

$\begin{array}{l} p_{1} V_{1} = ν R T, \\ p_{3} V_{3} = ν R T, \end{array}}$

где p ₃ — давление газа в конечном состоянии; V ₃ — объем газа в конечном состоянии.

Записанные уравнения состояния образуют систему уравнений

$\begin{array}{l} p_{1} V_{1} = ν R T, \\ p_{2} V_{2} = ν R T, \\ p_{3} V_{3} = ν R T, \end{array}}$

из которой следует найти отношение p ₃/p ₁ и подставить в выражение для η₂.

Деление первого и третьего уравнений дает

$\frac{p_{3}}{p_{1}} = \frac{V_{1}}{V_{3}}$

и сводит задачу к определению отношения объемов V ₁/V ₃.

Рассчитаем объемы газа в указанных состояниях.

Для расчета объемов V ₁ и V ₂ запишем пару уравнений состояния для первого процесса, дополнив ее равенством, определяющим ΔV ₁ = 1,0 л, т.е.

$\begin{array}{l} p_{1} V_{1} = ν R T, \\ p_{2} V_{2} = ν R T, \\ Δ V_{1} = V_{1} - V_{2} . \end{array}}$

Решение системы относительно V ₁ и V ₂ с учетом условия p ₂ = 1,2p ₁ дает значения:

V ₁ = 6,0 л;

V ₂ = 5,0 л.

Уравнение

ΔV ₂ = V ₁ − V ₃

с учетом значения ΔV ₂ = 2,0 л позволяет вычислить объем V ₃:

V ₃ = V ₁ − ΔV ₂ = 6,0 − 2,0 = 4,0 л.

Отношение давлений p ₃/p ₁ составляет

$\frac{p_{3}}{p_{1}} = \frac{6}{4} = 1,5$ ,

а искомая величина

$η_{2} = (\frac{p_{3}}{p_{1}} - 1) \cdot 100 % = (1,5 - 1) \cdot 100 % = 50 %$ .

Следовательно, при изотермическом сжатии газа на 2,0 л давление газа возрастает на 50 %.

Физика