Репетитор-онлайн — подготовка к ЦТ

2.3. Равнодействующая сил

2.3.1. Равнодействующая сил

Силу, заменяющую собой действие на тело нескольких сил, называют равнодействующей; равнодействующая сила равна векторной сумме сил, приложенных к данному телу:

$\vec{F} = {\vec{F}}_{1} + {\vec{F}}_{2} + ... + {\vec{F}}_{N}$ ,

где ${\vec{F}}_{1}$ , ${\vec{F}}_{2}$ , ..., ${\vec{F}}_{N}$ — силы, приложенные к данному телу.

Равнодействующую двух сил удобно находить графически по правилу параллелограмма (рис. 2.14, а) или треугольника (рис. 2.14, б).

Рис. 2.14

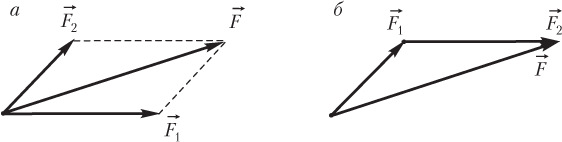
Для сложения нескольких сил (вычисления равнодействующей) используют следующий алгоритм:

1) вводят систему координат и записывают проекции всех сил на координатные оси:

F₁_x, F₂_x, ..., F_Nx,

F₁_y, F₂_y, ..., F_Ny;

2) вычисляют проекции равнодействующей как алгебраическую сумму проекций сил:

F_x = F₁_x + F₂_x + ... + F_Nx,

F_y = F₁_y + F₂_y + ... + F_Ny;

3) модуль равнодействующей вычисляют по формуле

$F = \sqrt{F_{x}^{2} + F_{y}^{2}}$ .

Рассмотрим частные случаи равнодействующей.

Силу взаимодействия тела с горизонтальной опорой, по которой может происходить движение тела, рассчитывают как равнодействующую силы трения и силы реакции опоры (рис. 2.15):

Рис. 2.15

${\vec{F}}_{вз} = {\vec{F}}_{тр} + \vec{N}$ ,

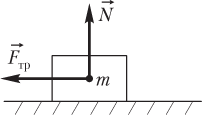
ее модуль вычисляется по формуле

$F_{вз} = \sqrt{F_{тр}^{2} + N^{2}}$ ,

где ${\vec{F}}_{тр}$ — сила трения скольжения или покоя; $\vec{N}$ — сила реакции опоры.

Частные случаи равнодействующей:

Силу взаимодействия тела с комбинированной опорой (например, креслом автомобиля, самолета и т.п.) рассчитывают как равнодействующую сил давления на вертикальную и горизонтальную части опоры (рис. 2.16):

${\vec{F}}_{вз} = {\vec{F}}_{гор} + {\vec{F}}_{верт}$ ,

где ${\vec{F}}_{гор}$ — сила давления, действующая на тело со стороны горизонтальной части опоры (численно равная весу тела); ${\vec{F}}_{верт}$ — сила давления, действующая на тело со стороны вертикальной части опоры (численно равная силе инерции).

Рис. 2.16

Частные случаи равнодействующей:

Равнодействующая силы тяжести и силы Архимеда называется подъемной силой (рис. 2.17):

${\vec{F}}_{под} = {\vec{F}}_{А} + m \vec{g}$ ,

ее модуль вычисляется по формуле

$F_{под} = F_{А} - m g$ ,

где ${\vec{F}}_{А}$ — сила Архимеда (выталкивающая сила); $m \vec{g}$ — сила тяжести.

Рис. 2.17

Частные случаи равнодействующей:

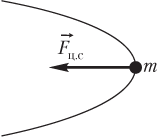
Если под влиянием нескольких сил тело равномерно движется по окружности, то равнодействующая всех приложенных к телу сил является центростремительной силой (рис. 2.18):

${\vec{F}}_{ц .с} = {\vec{F}}_{1} + {\vec{F}}_{2} + ... + {\vec{F}}_{N}$ .

где ${\vec{F}}_{1}$ , ${\vec{F}}_{2}$ , ..., ${\vec{F}}_{N}$ — силы, приложенные к телу.

Модуль центростремительной силы, направленной по радиусу к центру окружности, может быть вычислен по одной из формул:

$F_{ц .с} = \frac{m v^{2}}{R}$ , $F_{ц .с} = m ω^{2} R$ , $F_{ц .с} = m v ω$ ,

где m — масса тела; v — модуль линейной скорости тела; ω — величина угловой скорости; R — радиус окружности.

Рис. 2.18

Пример 21. По дну водоема, наклоненному под углом 60° к горизонту, начинает скользить тело массой 10 кг, полностью находящееся в воде. Найти модуль равнодействующей всех сил, приложенных к телу, если между телом и дном водоема воды нет, а коэффициент трения составляет 0,15.

Решение. Так как между телом и дном водяная прослойка отсутствует, то сила Архимеда на тело не действует.

Искомой величиной является модуль векторной суммы всех сил, приложенных к телу:

$\vec{F} = {\vec{F}}_{тр} + m \vec{g} + \vec{N}$ ,

где $\vec{N}$ — сила нормальной реакции опоры; $m \vec{g}$ — сила тяжести; ${\vec{F}}_{тр}$ — сила трения. Указанные силы и система координат изображены на рисунке.

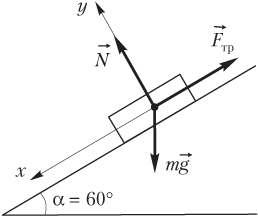
Вычисление модуля результирующей силы F проведем в соответствии с алгоритмом.

1. Определим проекции сил, приложенных к телу, на координатные оси:

на ось Ox:

проекция силы трения

$F_{тр x} = - F_{тр} = - μ N$ ;

проекция силы тяжести

${(m g)}_{x} = m g \sin 60 ° = 0,5 \sqrt{3} m g$ ;

проекция силы реакции опоры

N _x = 0;

на ось Оу:

проекция силы трения

$F_{тр y} = 0$ ;

проекция силы тяжести

${(m g)}_{y} = - m g \cos 60 ° = - 0,5 m g;$

проекция силы реакции опоры

N _y = N,

где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения.

2. Вычислим проекции равнодействующей на координатные оси, суммируя соответствующие проекции указанных сил:

$F_{x} = F_{тр x} + {(m g)}_{x} = - μ N + 0,5 \sqrt{3} m g$ ;

$F_{y} = {(m g)}_{y} + N_{y} = - 0,5 m g + N$ .

Движение по оси Oy отсутствует, т.е. F _y = 0, или, в явном виде:

$- 0,5 m g + N = 0$ .

Отсюда следует, что

$N = 0,5 m g$ ,

что позволяет получить формулу для расчета силы трения:

$F_{тр} = μ N = 0,5 μ m g$ .

3. Искомое значение равнодействующей:

$F = \sqrt{F_{x}^{2} + F_{y}^{2}} = | F_{x} | = - 0,5 μ m g + 0,5 \sqrt{3} m g = 0,5 m g (\sqrt{3} - μ)$ .

Произведем вычисление:

$F = 0,5 \cdot 10 \cdot 10 (\sqrt{3} - 0,15) = 79$ Н.

Пример 22. Тело массой 2,5 кг движется горизонтально под действием силы, равной 45 Н и направленной под углом 30° к горизонту. Определить величину силы взаимодействия тела с поверхностью, если коэффициент трения скольжения равен 0,5.

Решение. Силу взаимодействия тела и опоры найдем как равнодействующую силы трения ${\vec{F}}_{тр}$ и силы нормальной реакции опоры $\vec{N}$ :

${\vec{F}}_{вз} = {\vec{F}}_{тр} + \vec{N}$ ,

модуль которой определяется формулой

$F_{вз} = \sqrt{F_{тр}^{2} + N^{2}}$ .

Силы, приложенные к телу, показаны на рисунке.

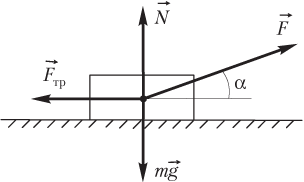
Модуль силы нормальной реакции опоры определяется формулой

$N = m g - F \sin 30 °$ ,

а модуль силы трения скольжения —

F _тр = µN,

где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения; F — модуль силы, вызывающей движение тела.

С учетом выражений для N и F _тр формула для расчета искомой силы принимает вид:

$F_{вз} = \sqrt{{(μ N)}^{2} + N^{2}} = N \sqrt{μ^{2} + 1} = (m g - F \sin 30 °) \sqrt{μ^{2} + 1}$ .

Выполним расчет:

$F_{вз} = (2,5 \cdot 10 - 45 \cdot 0,5) \sqrt{{(0,5)}^{2} + 1} \approx 2,8$ Н.

Пример 23. Во сколько раз изменится подъемная сила, если с аэростата сбросить балласт, равный половине его массы? Плотность воздуха считать равной 1,3 кг/м³, массу аэростата с балластом — 50 кг. Объем аэростата составляет 50 м³.

Решение. Подъемная сила, действующая на аэростат, является равнодействующей силы Архимеда ${\vec{F}}_{А}$ и силы тяжести $m \vec{g}$ :

${\vec{F}}_{под} = {\vec{F}}_{А} + m \vec{g}$ ,

модуль которой определяется формулой

F _под = F _A − mg,

где F _A = ρ_воздgV — модуль силы Архимеда; ρ_возд — плотность воздуха; g — модуль ускорения свободного падения; V — объем аэростата; m — масса аэростата (с балластом или без него).

Модуль подъемной силы может быть рассчитан по формулам:

для аэростата с балластом

$F_{под 1} = ρ_{возд} g V - m_{1} g$ ,

для аэростата без балласта

$F_{под 2} = ρ_{возд} g V - m_{2} g$ ,

где m ₁ — масса аэростата с балластом; m ₂ — масса аэростата без балласта.

Искомое отношение модулей подъемных сил составляет

$\frac{F_{под 2}}{F_{под 1}} = \frac{ρ_{возд} V - m_{2}}{ρ_{возд} V - m_{1}} = \frac{1,3 \cdot 50 - 25}{1,3 \cdot 50 - 50} \approx 2,7$ .

Пример 24. Модуль равнодействующей всех сил, действующих на тело, равен 2,5 Н. Определить в градусах угол между векторами скорости и ускорения, если известно, что модуль скорости остается постоянным.

Решение. Скорость тела не изменяется по величине. Следовательно, тело обладает только нормальной составляющей ускорения ${\vec{a}}_{n} \neq 0$ . Такой случай реализуется при равномерном движении тела по окружности.

Равнодействующая всех сил, приложенных к телу, является центростремительной силой и показана на рисунке.

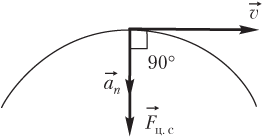
Векторы силы, скорости и ускорения имеют следующие направления:

центростремительная сила ${\vec{F}}_{ц .с}$ направлена к центру окружности;
вектор нормального ускорения ${\vec{a}}_{n}$ направлен так же, как и сила;
вектор скорости $\vec{v}$ направлен по касательной к траектории движения тела.

Следовательно, искомый угол между векторами скорости и ускорения равен 90°.

Физика