Физика

Общий тест

2.2. Силы

2.2.6. Сила инерции

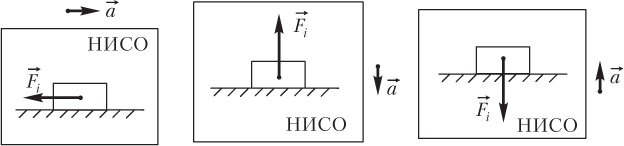
Сила инерции не является результатом взаимодействия данного тела с другими телами; ее появление связано с выбором системы отсчета.

Сила инерции вводится в рассмотрение только при решении задач в неинерциальных системах отсчета (НИСО), т.е. в системах отсчета, обладающих ускорением. В инерциальных системах отсчета (ИСО) силы инерции не действуют.

При решении задач в неинерциальной системе отсчета (НИСО), движущейся поступательно, сила инерции, действующая на тело массой m, определяется формулой

${\vec{F}}_{i} = - m \vec{a}$ ,

где $\vec{a}$ — ускорение НИСО (рис. 2.12).

Рис. 2.12

Модуль силы инерции рассчитывается как

F_i = ma;

ее направление всегда противоположно ускорению системы отсчета.

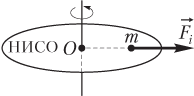
При решении задач в неинерциальной системе отсчета (НИСО), вращающейся с угловой скоростью ω по окружности радиусом R, модуль силы инерции, действующей на тело массой m, рассчитывается по формуле

$F_{i} = m ω^{2} R$ .

В этом случае F_i называется центробежной силой инерции; ее направление противоположно направлению центростремительной силы, т.е. она направлена по радиусу от центра окружности (рис. 2.13).

Рис. 2.13

Сила инерции в этом случае может быть вычислена также по формулам

$F_{i} = \frac{m v^{2}}{R}$ , $F_{i} = m v ω$ ,

где v — модуль линейной скорости.

Пример 19. При каком минимальном ускорении поезда книга, лежащая на горизонтальной поверхности, начнет скольжение? Коэффициент трения считать равным 0,5.

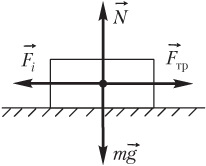
Решение. Силы, действующие на книгу, в неинерциальной системе отсчета, связанной с вагоном поезда, показаны на рисунке.

Силой, вызывающей скольжение книги, является сила инерции, модуль которой определяется формулой

F_i = ma,

где m — масса книги; a — модуль ускорения поезда.

Скольжение книги начнется при выполнении условия:

$F_{i} = F_{тр . пок}^{max}$ ,

где $F_{тр .пок}^{max} = μ N$ — модуль максимальной силы трения покоя; µ — коэффициент трения; N = mg — модуль силы нормальной реакции опоры; g — модуль ускорения свободного падения.

Из равенства

ma = µmg

следует, что

$a = μ g = 0,5 \cdot 10 = 5,0$ м/с².

Найденное значение ускорения соответствует минимальной силе инерции, следовательно, является минимальным.

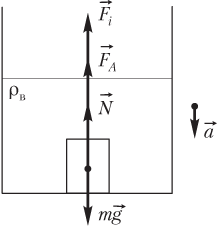
Пример 20. Тело, находящееся в сосуде с водой (ρ = 1000 кг/м³), поместили в лифт, опускающийся с ускорением, направленным вниз. При каком ускорении лифта тело станет невесомым? Тело имеет массу 100 г и занимает объем 10 см³. Между телом и дном сосуда существует водяная прослойка.

Решение. Силы, действующие на тело в сосуде с водой, помещенном в лифт, который движется с ускорением, показаны на рисунке.

Тело станет невесомым (P = 0), когда сила нормальной реакции опоры обратится в нуль:

$N = m g - F_{A} - F_{i} = 0$ ,

где F_A = ρ₀gV — модуль силы Архимеда; ρ₀ — плотность воды; g — модуль ускорения свободного падения; V — объем тела; F_i = ma — модуль силы инерции; m — масса тела; a — модуль ускорения лифта.

Из равенства

$m g - ρ_{0} g V - m a = 0$

следует, что искомая величина ускорения определяется формулой

$a = g (1 - \frac{ρ_{0} V}{m})$ .

Расчет дает значение:

$a = 10 \cdot (1 - \frac{10^{3} \cdot 10 \cdot 10^{- 6}}{100 \cdot 10^{- 3}}) = 9,0$ м/с².