Репетитор-онлайн — подготовка к ЦТ

13.3. Фотоэффект: волновая и квантовая теории

13.3.2. Уравнение Эйнштейна для внешнего фотоэффекта

В 1905 г. А. Эйнштейн объяснил фотоэффект с квантовых позиций.

Схема возникновения внешнего фотоэффекта представлена на рис. 13.4:

Рис. 13.4

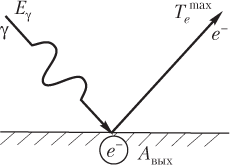
фотон с энергией E _γ, падая на вещество, передает часть своей энергии электрону, находящемуся вблизи поверхности вещества;
на отрыв электрона затрачивается энергия, равная работе выхода электрона из вещества A _вых;
вылетевший электрон обладает кинетической энергией $T_{e}^{max}$ .

Явление фотоэффекта описывается уравнением Эйнштейна, представляющим собой математическую запись закона сохранения энергии для фотоэффекта:

$E_{γ} = A_{вых} + T_{e}^{max}$ ,

где E _γ — энергия фотона; A _вых — работа выхода; $T_{e}^{max}$ — максимальная кинетическая энергия фотоэлектронов.

Энергия фотона E _γ рассчитывается по формулам:

E _γ = hν, $E_{γ} = \frac{h c}{λ}$ ,

где h — постоянная Планка, h = 6,626 ⋅ 10⁻³⁴ Дж ⋅ с; ν — частота фотона, ν = c/λ; λ — длина волны фотона; c — скорость света в вакууме, c ≈ 3,0 ⋅ 10⁸ м/с.

Работа выхода электронов из вещества A _вых является для данного вещества постоянной (справочной) величиной, не зависящей от характеристик излучения; она определяется только видом вещества и степенью обработки/чистоты его поверхности.

Максимальная кинетическая энергия фотоэлектронов $T_{e}^{max}$ вычисляется по формулам:

$T_{e}^{max} = \frac{m v_{max}^{2}}{2}$ , $T_{e}^{max} = | e | U_{з}$ ,

где m — масса электрона, m = 9,1 ⋅ 10⁻³¹ кг; v _max — максимальная скорость фотоэлектрона; |e| — модуль заряда электрона, |e| = 1,6 ⋅ 10⁻¹⁹ Кл; U _з — задерживающая разность потенциалов.

График зависимости максимальной кинетической энергии фотоэлектронов от частоты падающего на поверхность излучения представлен на рис. 13.5, а график зависимости задерживающего напряжения от указанной частоты — на рис. 13.6.

Рис. 13.5

Рис. 13.6

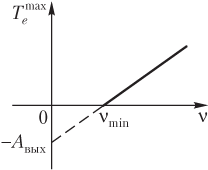
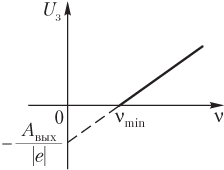
Квантовая теория полностью объясняет законы фотоэффекта:

1) число вырванных из поверхности фотоэлектронов пропорционально количеству поглощенных поверхностью фотонов, т.е. интенсивности излучения;

2) максимальная кинетическая энергия фотоэлектронов линейно зависит от частоты света (см. рис. 13.4):

$T_{e}^{max} = h ν - A_{вых}$ ,

где $T_{e}^{max}$ — максимальная энергия фотоэлектронов; h — постоянная Планка, h = 6,626 ⋅ 10⁻³⁴ Дж ⋅ с; A _вых — работа выхода; ν — частота фотона;

3) фотоэффект начинается, когда энергии фотона хватает, чтобы вырвать электрон из поверхности вещества (E _γ = A _вых); минимальной энергии соответствует минимальная частота света ν₀, названная «красной границей» фотоэффекта (см. рис. 13.4);

4) поглощение энергии фотона электроном происходит практически мгновенно, что объясняет безынерционность фотоэффекта.

Пример 7. Длина волны света, падающего на металлическую пластинку, уменьшилась от 500 до 420 нм. Определить работу выхода электрона, если известно, что максимальная кинетическая энергия фотоэлектронов увеличилась при этом в 2,50 раза.

Решение. При изменении режимов обучения работа выхода электронов из вещества не изменяется:

A _вых = const.

Запишем уравнение Эйнштейна дважды:

для света с длиной волны λ₁ —

E _γ1 = A _вых + T _e ₁,

где E _γ1 — энергия фотона, E _γ1 = hc/λ₁; h — постоянная Планка, h = 6,63 ⋅ 10⁻³⁴ Дж ⋅ с; c — скорость света в вакууме, c = 3,00 ⋅ 10⁸ м/с; T _e ₁ — максимальная кинетическая энергия фотоэлектронов в первом случае;

света с длиной волны λ₂ —

E _γ2 = A _вых + T _e ₂,

где E _γ2 — энергия фотона, E _γ2 = hc/λ₂; T _e ₂ — максимальная кинетическая энергия фотоэлектронов во втором случае.

Из уравнения Эйнштейна выразим максимальную кинетическую энергию фотоэлектронов:

для света с длиной волны λ₁ —

T _e ₁ = E _γ1 − A _вых;

света с длиной волны λ₂ —

T _e ₂ = E _γ2 − A _вых.

По условию задачи

T _e ₂ = 2,5T _e ₁,

или с учетом явного вида выражений для T _e ₁ и T _e ₂:

E _γ2 − A _вых = 2,5(E _γ1 − A _вых).

Выразим отсюда работу выхода электронов из вещества:

$A_{вых} = \frac{2,5 E_{γ 1} - E_{γ 2}}{1,5} = \frac{\frac{2,5 h c}{λ_{1}} - \frac{h c}{λ_{2}}}{1,5} = \frac{h c (2,5 λ_{2} - λ_{1})}{1,5 λ_{1} λ_{2}}$ .

Вычислим:

$A_{вых} = \frac{6,63 \cdot 10^{- 34} \cdot 3,00 \cdot 10^{8} (2,5 \cdot 420 \cdot 10^{- 9} - 500 \cdot 10^{- 9})}{1,5 \cdot 420 \cdot 500 \cdot 10^{- 18}} =$

$= 3,47 \cdot 10^{- 19}$ Дж.

Выполним перевод полученного значения работы выхода из джоулей в электронвольты:

$A_{вых} \approx \frac{3,47 \cdot 10^{- 19}}{1,6 \cdot 10^{- 19}} = 2,17$ эВ.

Работа выхода электронов из поверхности данного вещества составляет 2,17 эВ.

Физика