Репетитор-онлайн — подготовка к ЦТ

4.1. Элементы статики

4.1.7. Некоторые простые механизмы: блоки

Устройства, предназначенные для перемещения (подъема, опускания) грузов с помощью колеса и перекинутой через него нити, к которой приложена некоторая сила, называются блоками. Различают неподвижные и подвижные блоки.

Блоки предназначены для перемещения груза весом $\vec{P}$ c помощью силы $\vec{F}$ , приложенной к веревке, перекинутой через колесо.

Для любых типов блоков (неподвижных и подвижных) выполняется условие равновесия:

d₁F = d₂P,

где d₁ — плечо силы $\vec{F}$ , приложенной к веревке; d₂ — плечо силы $\vec{P}$ (веса груза, перемещаемого при помощи данного блока).

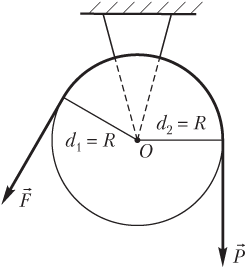
В неподвижном блоке (рис. 4.8) плечи сил $\vec{F}$ и $\vec{P}$ одинаковы и равны радиусу блока:

d₁ = d₂ = R,

где d₁ — плечо силы $\vec{F}$ , приложенной к веревке; d₂ — плечо силы $\vec{P}$ (веса груза, перемещаемого при помощи данного блока),

поэтому модули сил равны между собой:

F = P.

Рис. 4.8

С помощью неподвижного блока тело весом $\vec{P}$ можно переместить, прикладывая силу $\vec{F}$ , величина которой совпадает с величиной веса груза.

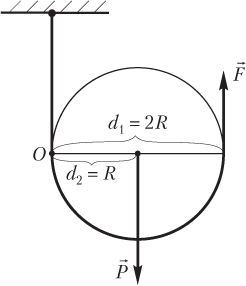
В подвижном блоке (рис. 4.9) плечи сил $\vec{F}$ и $\vec{P}$ различны:

d₁ = 2R и d₂ = R,

где d₁ — плечо силы $\vec{F}$ , приложенной к веревке; d₂ — плечо силы $\vec{P}$ (веса груза, перемещаемого при помощи данного блока),

поэтому модули сил подчиняются равенству:

$F = \frac{P}{2}$ .

Рис. 4.9

С помощью подвижного блока тело весом $\vec{P}$ можно переместить, прикладывая силу $\vec{F}$ , величина которой вдвое меньше величины веса груза.

Блоки позволяют переместить тело на некоторое расстояние:

неподвижный блок не дает выигрыша в силе; он лишь изменяет направление приложенной силы;
подвижный блок дает выигрыш в силе в 2 раза.

Однако и подвижный, и неподвижный блоки не дают выигрыша в работе: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии («золотое правило» механики).

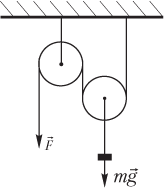
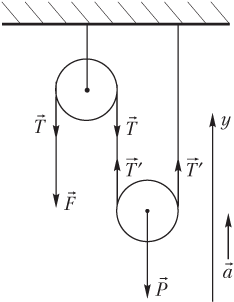
Пример 22. Система состоит из двух невесомых блоков: одного подвижного и одного неподвижного. Груз массой 0,40 кг подвешен к оси подвижного блока и касается пола. К свободному концу веревки, перекинутой через неподвижный блок, прикладывают некоторую силу так, как показано на рисунке. Под действием этой силы груз поднимается из состояния покоя на высоту 4,0 м за 2,0 с. Найти модуль силы, приложенной к веревке.

Решение. Силы, действующие на подвижный и неподвижный блоки, показаны на рисунке.

На неподвижный блок со стороны веревки действуют две силы $\vec{T}$ (по обе стороны от блока); под действием указанных сил поступательное движение блока отсутствует. Каждая из указанных сил равна силе $\vec{F}$ , приложенной к концу веревки:

$\vec{T} = \vec{F}$ .

На подвижный блок действуют три силы: две силы натяжения веревки ${\vec{T}}^{'}$ (по обе стороны от блока) и вес груза $\vec{P} = m \vec{g}$ ; под действием указанных сил блок (вместе с подвешенным к нему грузом) движется вверх с ускорением.

Запишем второй закон Ньютона для подвижного блока в виде:

$2 {\vec{T}}^{'} + \vec{P} = m \vec{a}$ ,

или в проекции на координатную ось, направленную вертикально вверх,

$2 T^{'} - m g = m a$ ,

где $T^{'}$ — модуль силы натяжения веревки; m — масса груза (масса подвижного блока с грузом); g — модуль ускорения свободного падения; a — модуль ускорения блока (груз имеет такое же ускорение, поэтому далее будем говорить об ускорении груза).

Модуль силы натяжения веревки $T^{'}$ равен модулю силы T:

$T^{'} = T = F$ ,

поэтому модуль ускорения груза определяется выражением

$a = \frac{2 F - m g}{m}$ .

Пройденный грузом путь совпадает с его высотой над поверхностью пола и связан с временем его движения t формулой

$h = \frac{a t^{2}}{2}$ ,

или с учетом выражения для модуля ускорения

$h = \frac{a t^{2}}{2} = \frac{(2 F - m g) t^{2}}{2 m}$ .

Выразим отсюда искомую силу:

$F = m (\frac{h}{t^{2}} + \frac{g}{2})$

и рассчитаем ее значение:

$F = 0,40 (\frac{4,0}{{(2,0)}^{2}} + \frac{10}{2}) = 2,4$ Н.

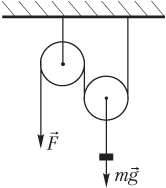
Пример 23. Система состоит из двух невесомых блоков: одного подвижного и одного неподвижного. Некоторый груз подвешен к оси неподвижного блока так, как показано на рисунке. Под действием постоянной силы, приложенной к свободному концу веревки, груз начинает двигаться с постоянным ускорением и перемещается вверх на расстояние 3,0 м за 2,0 с. За время движения груза приложенная сила развивает среднюю мощность 12 Вт. Найти массу груза.

Решение. Силы, действующие на подвижный и неподвижный блоки, показаны на рисунке.

На неподвижный блок со стороны веревки действуют две силы $\vec{T}$ (по обе стороны от блока); под действием указанных сил поступательное движение блока отсутствует. Каждая из указанных сил равна силе $\vec{F}$ , приложенной к концу веревки:

$\vec{T} = \vec{F}$ .

На подвижный блок действуют три силы: две силы натяжения веревки ${\vec{T}}^{'}$ (по обе стороны от блока) и вес груза $\vec{P} = m \vec{g}$ ; под действием указанных сил блок (вместе с подвешенным к нему грузом) движется вверх с ускорением.

Запишем второй закон Ньютона для подвижного блока в виде:

$2 {\vec{T}}^{'} + \vec{P} = m \vec{a}$ ,

или в проекции на координатную ось, направленную вертикально вверх,

$2 T^{'} - m g = m a$ ,

где $T^{'}$ — модуль силы натяжения веревки; m — масса груза (масса подвижного блока с грузом); g — модуль ускорения свободного падения; a — модуль ускорения блока (груз имеет такое же ускорение, поэтому далее будем говорить об ускорении груза).

Модуль силы натяжения веревки $T^{'}$ равен модулю силы T:

$T^{'} = T = F$ ,

поэтому модуль ускорения груза определяется выражением

$a = \frac{2 F - m g}{m}$ .

С другой стороны, ускорение груза определяется формулой для пройденного пути:

$S = \frac{a t^{2}}{2}$ ,

т.е.

$a = \frac{2 S}{t^{2}}$ ,

где t — время движения груза.

Равенство

$\frac{2 F - m g}{m} = \frac{2 S}{t^{2}}$

позволяет получить выражение для модуля приложенной силы:

$F = m (\frac{S}{t^{2}} + \frac{g}{2})$ .

Груз движется равноускоренно, поэтому модуль его скорости определяется выражением

v = at,

а средняя скорость движения —

$〈 v 〉 = \frac{S}{t} = \frac{a t}{2}$ .

Величина средней мощности, развиваемой приложенной силой, определяется формулой

$〈 N 〉 = F 〈 v 〉$ ,

или с учетом выражений для модуля силы и средней скорости:

$〈 N 〉 = \frac{m a (2 S + g t^{2})}{4 t}$ .

Отсюда выразим искомую массу:

$m = \frac{4 t 〈 N 〉}{a (2 S + g t^{2})}$ .

Подставим в полученную формулу выражение для ускорения (a = 2S/t²):

$m = \frac{2 t^{3} 〈 N 〉}{S (2 S + g t^{2})}$

и произведем расчет:

$m = \frac{2 \cdot {(2,0)}^{3} \cdot 12}{3,0 (2 \cdot 3,0 + 10 \cdot {(2,0)}^{2})} \approx 1,4$ кг.

Физика