Физика

Пример 5. В ходе изотермического расширения газу сообщили 64 Дж теплоты. При дальнейшем изотермическом расширении газом совершена работа 18 Дж. Определить работу газа в ходе всего процесса.

Решение. Работа газа в ходе всего процесса является суммой

A = A ₁ + A ₂,

где A ₁ — работа, совершенная газом в первом процессе; A ₂ — работа, совершенная газом во втором процессе.

Оба процесса, происходящие в газе, являются изотермическими; работа, совершенная газом, определяется следующим образом:

• в первом процессе — с помощью первого начала термодинамики —

A ₁ = Q ₁ − ΔU ₁,

где Q ₁ — количество теплоты, сообщенной газу в первом процессе; ΔU ₁ — изменение внутренней энергии газа в изотермическом процессе, ΔU ₁ = 0;

• во втором процессе — задана в условии задачи —

A ₂ = 18 Дж.

Таким образом, искомая работа газа определяется формулой

A = Q ₁ + A ₂

и составляет

A = 64 + 18 = 82 Дж.

Пример 6. При изотермическом расширении 5,0 моль идеального газа сообщено 1,60 кДж теплоты. Затем газ перевели в первоначальное состояние путем изобарного сжатия и изохорного нагревания. Работа газа за цикл равна 769 Дж. Определить разность минимальной и максимальной температур в цикле.

Решение. Работа газа за цикл является суммой

A = A ₁ + A ₂ + A ₃,

где A ₁ — работа, совершенная газом при изотермическом расширении; A ₂ — работа, совершенная газом при изобарном сжатии; A ₃ — работа, совершенная газом при изохорном нагревании.

Работа, совершенная газом в каждом из процессов, определяется следующим образом:

• при изотермическом расширении — с помощью первого начала термодинамики —

A ₁ = Q ₁ − ΔU ₁,

где Q ₁ — количество теплоты, переданное газу при изотермическом процессе; ∆U ₁ — изменение внутренней энергии газа при изотермическом процессе, ∆U ₁ = 0;

• при изобарном сжатии — с помощью формулы для вычисления работы газа при изобарном процессе –

A ₂ = νR(T ₂ − T ₁),

где ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T ₁ — начальная температура газа; T ₂ — температура газа в конце изобарного сжатия;

• при изохорном нагревании —

A ₂ = 0,

так как при изохорном процессе работа не совершается.

Таким образом, работа газа за цикл определяется формулой

A = Q ₁ + νR(T ₂ − T ₁).

Проанализируем изменение температуры газа за цикл:

• при изотермическом расширении — температура газа не изменяется —

T ₁ = const;

• при изобарном сжатии — температура газа понижается от T ₁ до T ₂ —

T ₂ < T ₁,

так как выполняется равенство

$\frac{V_1}{V_2}=\frac{T_1}{T_2}<1$;

• при изохорном нагревании — температура повышается от T ₂ до T ₁ по условию задачи.

Температура T ₁ является максимальной, а температура T ₂ — минимальной температурой газа в цикле:

T _max = T ₁, T _min = T ₂.

С учетом этого работа газа за цикл определяется выражением

$A=Q_1+\nu R(T_{\text{min}}-T_{\text{max}})=Q_1-\nu R(T_{\text{max}}-T_{\text{min}})$

и позволяет рассчитать искомую разность температур:

$T_{\text{max}}-T_{\text{min}}=\frac{Q_1-A}{\nu R}=\frac{\mathrm{1,60}\cdot {10}^3-769}{\mathrm{5,0}\cdot \mathrm{8,31}}=20$ К.

Разность максимальной и минимальной температур в указанном цикле составляет 20 К.

Пример 7. Абсолютная температура 5,00 моль идеального одноатомного газа меняется по закону: T = V ²/R, где V — объем газа в кубических метрах; R — универсальная газовая постоянная. Какое количество теплоты нужно сообщить газу в ходе этого процесса для нагревания его на 10,0 К?

Решение. Количество теплоты, необходимое для нагревания газа, определяется первым началом термодинамики:

Q = A + ΔU,

где A — работа, совершенная газом в указанном процессе; ΔU — изменение внутренней энергии газа.

Для определения количества теплоты необходимо рассчитать работу, совершенную газом, и изменение его внутренней энергии.

Чтобы рассчитать работу, совершенную газом, необходимо установить зависимость давления газа p от его объема V, т.е. p(V). Для этого из уравнения состояния

pV = νRT

выразим температуру

$T=\frac{pV}{\nu R}$

и подставим ее в заданный в условии задачи закон:

$\frac{pV}{\nu R}=\frac{V^2}{R}$.

Преобразование дает линейную зависимость

p = νV.

На рисунке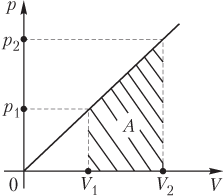 показана полученная зависимость и соответствующие изменения объема и давления газа при изменении его температуры на ΔT; заштрихованная площадь (трапеция) соответствует искомой работе газа:

$A=\frac{1}{2}(p_1+p_2)(V_2-V_1)$,

где p ₁, V ₁ — давление и объем газа при температуре T ₁; p ₂, V ₂ — давление и объем газа при температуре T ₂.

Зависимость p(V) позволяет определить начальное и конечное давления газа в ходе процесса:

• начальное давление —

p ₁ = νV ₁;

• конечное давление —

p ₂ = νV ₂.

Подстановка выражений для давления в формулу работы дает

$A=\frac{\nu }{2}(V_1+V_2)(V_2-V_1)=\frac{1}{2}(\nu V_2^2-\nu V_1^2)$.

Зависимость температуры от объема, заданная в условии задачи, позволяет преобразовать формулу к виду

$A=\frac{1}{2}(\nu V_2^2-\nu V_1^2)=\frac{1}{2}(\nu R{T}_2-\nu R{T}_1)=\frac{1}{2}\nu R\Delta T$.

Чтобы рассчитать изменение внутренней энергии идеального одноатомного газа, воспользуемся формулой

$\Delta U=\frac{3}{2}\nu R\Delta T$.

Таким образом, количество теплоты, которое следует сообщить газу для указанного повышения температуры, определяется выражением

$Q=A+\Delta U=\frac{1}{2}\nu R\Delta T+\frac{3}{2}\nu R\Delta T=2\nu R\Delta T$

и составляет

Q = 2 ⋅ 5,00 ⋅ 8,31 ⋅ 10,0 = 831 Дж.

Пример 8. Для повышения температуры 20,0 кг смеси идеальных газов со средней молярной массой 25,0 г/моль на 40,0 К при постоянном давлении необходимо затратить 500 кДж теплоты. Какое количество теплоты следует отвести от указанной смеси газов при постоянном объеме, чтобы ее температура понизилась на 40,0 К?

Решение. Запишем первое начало термодинамики для указанных в условии процессов:

• для изобарного нагревания —

Q ₁ = A ₁ + ΔU ₁,

где Q ₁ — количество подведенной к газу (смеси газов) теплоты; A ₁ — работа, совершенная газом при изобарном нагревании, A ₁ = νRΔT; ν — количество вещества, ν = m/M; m — масса смеси; M — средняя молярная масса смеси; R — универсальная газовая постоянная, R = = 8,31 Дж/(моль ⋅ К); ΔT — увеличение температуры смеси; i — число степеней свободы; ΔU ₁ — увеличение внутренней энергии смеси при изобарном нагревании, ΔU ₁ = iνRΔT/2;

• для изохорного охлаждения —

Q ₂ = A ₂ + ΔU ₂,

где Q ₂ — количество отведенной теплоты, Q ₂ < 0; A ₂ — работа, совершенная смесью при изохорном охлаждении, A ₂ = 0; ΔU ₂ — уменьшение внутренней энергии смеси при изохорном охлаждении, ΔU ₂ = iνRΔT/2 < 0.

Уравнения, соответствующие первому началу термодинамики для изобарного нагревания и изохорного охлаждения, записанные в явном виде, образуют систему

$\begin{array}{l}{Q}_1=\nu R\Delta T+\frac{i}{2}\nu R\Delta T,\\ -\left|Q_2\right|=-\frac{i}{2}\nu R\Delta T\text{,}\end{array}\}$

которую необходимо решить относительно |Q ₂|.

Сложение уравнений дает

$Q_1-\left|Q_2\right|=\nu R\Delta T+\frac{i}{2}\nu R\Delta T-\frac{i}{2}\nu R\Delta T=\nu R\Delta T$,

или, после упрощения, —

$Q_1-\left|Q_2\right|=\frac{m}{M}R\Delta T$.

Выразим отсюда искомую величину

$\left|Q_2\right|=Q_1-\frac{m}{M}R\Delta T$

и произведем вычисление:

$\left|Q_2\right|=500\cdot {10}^3-\frac{\mathrm{20,0}}{\mathrm{25,0}\cdot {10}^{-3}}\cdot \mathrm{8,31}\cdot \mathrm{40,0}=234\cdot {10}^3\text{ Дж}=234$ кДж.

Следовательно, для изохорного охлаждения газа на 40,0 К необходимо отвести от смеси газов 234 кДж теплоты.